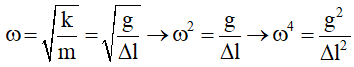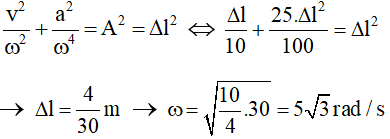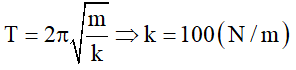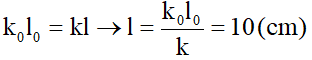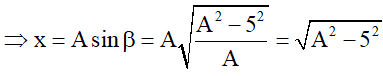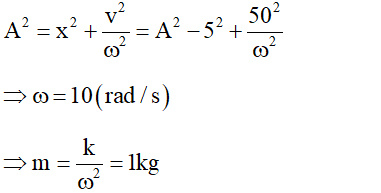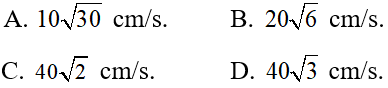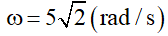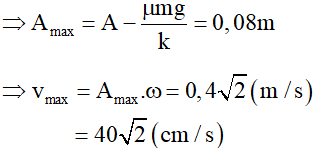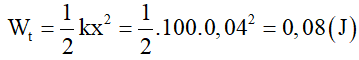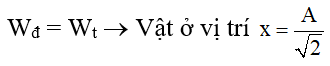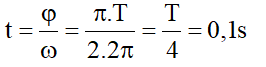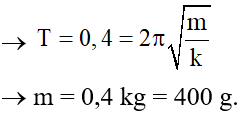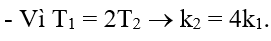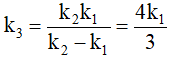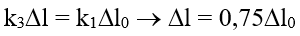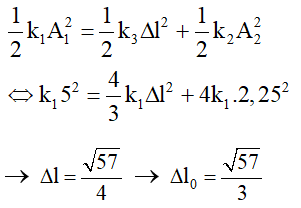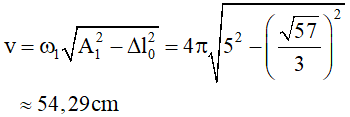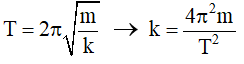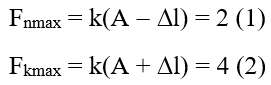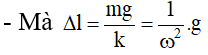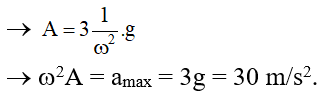Bộ 40 bài tập trắc nghiệm Vật Lí lớp 12 Bài 2 : Con lắc lò xo có đáp án không thiếu những mức độ giúp những em ôn trắc nghiệm Vật Lí 12 Bài 2 .
Bài giảng Vật Lí 12 Bài 2: Con lắc lò xo
Câu 1. Nhận xét nào sau đây là đúng khi nói đến đặc điểm của lực kéo về?
A. Lực luôn hướng về vị trí cân đối gọi là lực kéo về .Quảng cáoB. Có độ lớn tỉ lệ với li độ .
C. Là lực gây ra tần suất cho vật xê dịch điều hòa .
D. Cả A, B và C đều đúng .
Hiển thị đáp án
Đáp án: D
Giải thích : Lực kéo về có biểu thức F = – kx
+ Lực luôn hướng về vị trí cân đối gọi là lực kéo về .
+ Lực kéo về có độ lớn tỉ lệ với li độ .
+ Lực gây ra tần suất cho vật giao động điều hòa .
Câu 2. Một con lắc lò xo đang dao động điều hòa. Nhận xét nào sau đây không đúng?
A. Cơ năng của con lắc tỉ lệ với biên độ xê dịch .Quảng cáoB. Cơ năng của con lắc tỉ lệ với bình phương của biên độ xê dịch .
C. Cơ năng của con lắc được bảo toàn nếu bỏ lỡ mọi ma sát .
D. Động năng của con lắc biến thiên tuần hoàn theo thời hạn .
Hiển thị đáp án
Đáp án: A
Giải thích : Biểu thức cơ năng : W = 12 mω2A2
A – sai, vì cơ năng của con lắc lò xo tỉ lệ với bình phương của biên độ giao động .
B – đúng
C – đúng
D – đúng
Câu 3. Công thức tính chu kì dao động của con lắc lò xo là
A. T = πmk .
B. T = 2 πkm .
C. T = 2 πmk .
D. T = 12 πmk .
Hiển thị đáp án
Đáp án: C
Giải thích : Chu kì xê dịch của con lắc lò xo là : T = 2 πmk
Câu 4. Trong dao động điều hòa của con lắc lò xo, lực kéo về tác dụng lên vật
A. tỉ lệ với độ biến dạng của lò xo .
B. tỉ lệ với khoảng cách từ vật đến vị trí cân đối .
C. luôn hướng ra xa vị trí cân đối .
D. luôn tỉ lệ nghịch với độ biến dạng của lò xo .
Hiển thị đáp án
Đáp án: B
Giải thích :
A – Sai, vì lực kéo về chỉ tỉ lệ với độ biến dạng của lò xo khi lò xo nằm ngang .
B – Đúng
C – Sai, vì lực kéo về luôn hướng về vị trí cân đối .
D – Sai, vì lực kéo về chỉ tỉ lệ với độ biến dạng của lò xo khi lò xo nằm ngang .
Câu 5. Một con lắc lò xo gồm vật nhỏ có khối lượng m gắn với một lò xo nhẹ có độ cứng k. Con lắc này có tần số dao động riêng là
A. f = 12 πmk .
B. f = 12 πkm .
C. f = 2 πmk .
D. f = 2 πkm .
Hiển thị đáp án
Đáp án: B
Giải thích : Tần số xê dịch riêng của con lắc là f = 1T = 12 πkm .
Câu 6. Chu kì của con lắc phụ thuộc vào
A. khối lượng vật và độ cứng của lò xo .
B. tần suất trọng trường tại nơi làm thí nghiệm .
C. khối lượng vật .
D. độ cứng của lò xo .
Hiển thị đáp án
Đáp án: A
Giải thích : Chu kì của con lắc lò xo nhờ vào vào khối lượng vật và độ cứng của lò xo .
Câu 7. Một con lắc lò xo gồm vật có khối lượng m và lò xo có độ cứng k không đổi, dao động điều hoà. Nếu khối lượng 200 g thì chu kì dao động của con lắc là 2 s. Để chu kì con lắc là 1 s thì khối lượng m bằng
A. 10 g .
B. 20 g .
C. 35 g .
D. 50 g .
Hiển thị đáp án
Đáp án: D
Giải thích :
Chu kì giao động của con lắc được tính bởi công thức : T = 2 πmk
Ta có :
T2T1 = 2 πm2k2πm1k = m2m1 ⇒ 12 = m2200 ⇒ mét vuông = 50 gam
Câu 8. Một vật nhỏ m lần lượt liên kết với các lò xo có độ cứng k1, k2 và k thì chu kỳ dao động lần lượt bằng T1 = 1,6s, T2 = 1,8 s và T. Nếu k2=2k12+5k22 thì T bằng
A. 1,4 s .
B. 2,0 s .
C. 2,5 s .
D. 1,1 s .
Hiển thị đáp án
Đáp án: D
Giải thích : T tỉ lệ nghịch với k hay k2 tỉ lệ nghịch với T4 nên từ hệ thức k2 = 2 k12 + 5 k22 suy ra
1T4 = 2.1 T14 + 5.1 T24 ⇒ T = T1T22T22 + 5T144 ≈ 1,1 s
Câu 9. Một con lắc lò xo gồm lò xo có độ cứng 20 N/m và viên bi có khối lượng dao động điều hòa. Tại thời điểm t, vận tốc, gia tốc của viên bi lần lượt là 20 cm/s và 23 m/s2 . Biên độ dao động của viên bi là
A. 2 cm .
B. 4 cm .
C. 5 cm .
D. 7 cm .
Hiển thị đáp án
Đáp án: B
Giải thích : Tần số góc là : ω = km = 10 rad / s
Li độ tại thời gian t là : a = − xω2 ⇒ x = − aω2 = − 23 ( cm )
Biên độ xê dịch : A = x2 + v2ω2 = ( − 23 ) 2 + ( 2010 ) 2 = 4 ( cm )
Câu 10. Một lò xo dãn ra khi treo vào nó một vật có khối lượng 250 g. Chu kì của con lắc được tạo thành như vậy là bao nhiêu? Cho g=10m/s2.
A. 1,1 s .
B. 0,95 s .
C. 0,53 s .
D. 0,31 s .
Hiển thị đáp án
Đáp án: D
Giải thích : Ở vị trí cân đối thì : Fdh = P ⇔ kΔlo = mg ⇔ km = gΔlo
Chu kì xê dịch của con lắc : T = 2 πΔl0g = 2 π2, 5.10 − 210 = 0,31 ( s )
Câu 11. Một con lắc lò xo có cơ năng W = 0,9 J và biên độ dao động A = 15cm. Hỏi động năng của con lắc tại vị trí có li độ x = -5 cm là bao nhiêu?
A. 0,5 J .
B. 0,8 J .
C. 0,95 J .
D. 1 J .
Hiển thị đáp án
Đáp án: B
Giải thích :
Độ cứng của lò xo : W = 12 kA2 ⇒ k = 2WA2 = 2.0,915. 10 − 22 = 80 ( N / m )
Động năng của con lắc tại vị trí x = − 5 cm là :
Wđ = W − Wt = W − 12 kx2 = 0,9 − 12.80. − 5.10 − 22 = 0,8 J
Câu 12. Một con lắc lò xo có độ cứng k = 200N/m, khối lượng m = 200 g dao động điều hòa với biên độ A=10(cm). Tốc độ của con lắc khi qua vị trí có li độ x = 2,5 cm là bao nhiêu?
A. 1,55 m / s .
B. 0,97 m / s .
C. 2,52 m / s .
D. 3,06 m / s .
Hiển thị đáp án
Đáp án: D
Giải thích : Tần số góc của xê dịch : ω = km = 1010 ( rad / s )
Tốc độ của con lắc khi nó đi qua vị trí x = 2,5 cm là :
v = ωA2 − x2 = 101010.10 − 22 − 2,5. 10 − 22 = 3,06 ( m / s )
Câu 13. Một con lắc lò xo dao động điều hòa. Lò xo có độ cứng k = 80 N/m. Trong một chu kì, con lắc đi được một đoạn đường dài 20 cm. Cơ năng của con lắc là
A. 0,1 J .
B. 0,2 J .
C. 0,3 J .
D. 0,4 J .
Hiển thị đáp án
Đáp án: A
Giải thích :
Quãng đường vật đi được trong một chu kì là : ST = 4A ⇒ A = 5 cm
Cơ năng của con lắc : W = 12 kA2 = 0,1 J
Câu 14. Chất điểm có khối lượng m1 = 50 g dao động điều hoà quanh vị trí cân bằng của nó với phương trình dao động x1=5cosπt+π6(cm). Chất điểm có khối lượng m2 = 100g dao động điều hoà quanh vị trí cân bằng của nó với phương trình dao động x2=5cosπt−π6(cm). Tỉ số cơ năng trong quá trình dao động điều hoà của chất điểm m1 so với chất điểm m2 bằng
A. 0,25 .
B. 0,5 .
C. 1 .
D. 2 .
Hiển thị đáp án
Đáp án: B
Giải thích : Tỉ số cơ năng giữa hai con lắc là :
W1W2 = 12 m1ω12A1212m2ω22A22 = 1250. π2. 5212100. π2. 52 = 12
Câu 15. Con lắc lò xo dao động điều hoà với tần số 2 Hz, khối lượng quả nặng là 100 g, lấy π2=10. Độ cứng của lò xo là
A. 8 N / m .
B. 80 N / m .
C. 16 N / m .
D. 160 N / m .
Hiển thị đáp án
Đáp án: C
Giải thích : Ta có : f = 12 πkm ⇒ k = ( 2 πfm ) 2
= 4 π2f2m = 4.10.22. 0,1 = 16 ( N / m )
Câu 16. Một con lắc lò xo đang dao động điều hòa theo phương ngang với biên độ cm. Vật nhỏ của con lắc có khối lượng 100g, lò xo có độ cứng 100 N/m. Khi vật nhỏ có vận tốc 1010 cm/s thì gia tốc của nó có độ lớn là
A. 103 m / s2 .
B. 3 m / s2 .
C. 53 m / s2 .
D. 23 m / s2 .
Hiển thị đáp án
Đáp án: A
Giải thích : Tần số góc của xê dịch là : ω = km = 1010 ( rad / s )
Áp dụng công thức độc lập thời hạn cho hai đại lượng vuông pha a và v ta được :
vωA2 + aω2A2 = 1
⇒ a = ω2A1 − vωA2 = 103 ( m / s2 )
Câu 17. Một con lắc lò xo gồm vật nặng 0,2 kg gắn vào đầu lò xo có độ cứng 20 N/m. Kéo quả nặng ra khỏi vị trí cân bằng rồi thả nhẹ cho nó dao động, tốc độ trung bình trong 1 chu kỳ là 160π cm/s. Cơ năng dao dao động của con lắc là
A. 0,025 J .
B. 0,064 J .
C. 0,072 J .
D. 0,095 J .
Hiển thị đáp án
Đáp án: B
Giải thích : Ta có :
T = 2 πmk = π5sv ¯ = 4AT ⇒ 160 π = 4A π5 ⇒ A = 8 cm
Câu 18. Con lắc lò xo dao động điều hòa với phương trình: x = Acosωt. Thời điểm lần thứ hai thế năng bằng 3 lần động năng là
A. 5 π6ωs .
B. π6ωs .
C. 5 π3ωs .
D. πωs .
Hiển thị đáp án
Đáp án: A
Giải thích : Ta có :
x1 = AWt = 3W d = 34W ⇒ kx22 = 34 kA22
⇒ x2 = ± A32
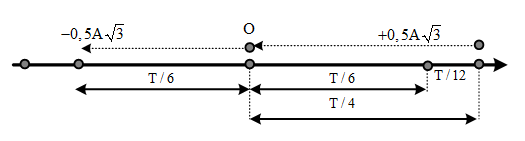
+ Lần 1 : Wt = 3W đ là đi từ x = A đến x = A32 ⇒ t2 = 112T = π6ω ( s )
+ Lần 2 : Wt = 3W đ là đi từ x = A đến x = − A32 ⇒ t1 = T4 + T6 = 512T = 5 π6ω ( s )
Câu 19. Một con lắc lò xo gồm lò xo nhẹ và vật nhỏ khối lượng 100g đang dao động điều hòa theo phương ngang, mốc tính thế năng tại vị trí cân bằng. Từ thời điểm t1 = 0s đến t2=π48s, động năng của con lắc tăng từ 0,096 J đến giá trị cực đại rồi giảm về 0,064 J. Ở thời điểm t2, thế năng của con lắc bằng 0,064 J. Biên độ dao động của con lắc là
A. 6 cm .
B. 7 cm .
C. 8 cm .
D. 9 cm .
Hiển thị đáp án
Đáp án: C
Giải thích :
Tại thời gian t2 động năng bằng thế năng : x2 = A2W = Wtt2 + Wđt2 = 0,128 J
Tại thời gian t1 = 0 thì Wđ = 0,096 = 3W4 ; Wt = W4 nên lúc này x0 = ± A2
Ta hoàn toàn có thể trình diễn quy trình hoạt động như trên hình vẽ sau :
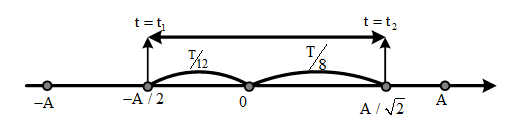
Ta có : t1 = T12 + T8 = π48s ⇒ T = 0,1 π ( s )
⇒ ω = 2 πT = 20 rad / s
Biên độ tính từ công thức : W = mω2A22
⇒ A = 2W mω2 = 2.0,1280, 1.202 = 0,08 m = 8 cm
Câu 20. Một con lắc lò xo dao động điều hòa trên mặt phẳng ngang gồm lò xo có độ cứng 100 N/m và vật dao động nặng 0,1 kg. Khi t = 0 vật qua vị trí cân bằng với tốc độ 40π (cm/s). Đến thời điểm t = 130 s người ta giữ cố định điểm chính giữa của lò xo. Biên độ dao động mới của vật là
A. 5 cm .
B. 5 cm .
C. 3 cm .
D. 3 cm .
Hiển thị đáp án
Đáp án: B
Giải thích : Ta có :
T = 2 πmk = 0,2 s ; ω = 2 πT = 10 πrad / s
⇒ A = vcbω = 4 cm
t = 130 s = T6 ⇒ x = A32 = 23 cm
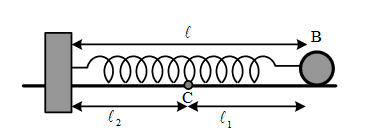
Phần phần thế năng bị nhốt : Wnhot = l2lkx22
Cơ năng còn lại : W ‘ = W − Wnhot ⇔ k1A122 = kA22 − l2lkx22
A1 = kk1A2 − l2lkk1x2 với kk1 = l1l = 12 ; l2l = 12
⇒ A1 = 1242 − 12.12232 = 5 cm
Câu 21. Một lò xo nhẹ có chiều dài tự nhiên 30 cm có độ cứng là k, đầu trên cố định, đầu dưới gắn vật m, vật dao động điều hoà trên mặt phẳng nghiêng góc 30° với phương trình x=6cos10t+5π6cm (t đo bằng s) tại nơi có g = 10 m/s2. Trong quá trình dao động chiều dài cực tiểu của lò xo là
A. 20 cm .
B. 27 cm .
C. 29 cm .
D. 37 cm .
Hiển thị đáp án
Đáp án: C
Giải thích :
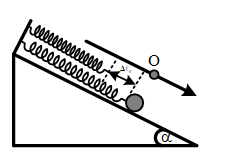
Độ dãn của lò xo khi vật ở VTCB :
Δl0 = mgsinαk = g. sinαω2 = 0,05 m
Chiều dài lò xo tại VTCB ( l0 là chiều dài tự nhiên ) : lCB = l0 + Δl0 = 35 cm
Chiều dài cực tiểu ( khi vật ở vị trí cao nhất ) : lmin = lcb − A = 29 cm
Câu 22. Một con lắc lò xo treo thẳng đứng, vật treo có khối lượng m. Kéo vật xuống dưới vị trí cân bằng 3 cm rồi truyền cho nó vận tốc 40 cm/s thì nó dao động điều hòa theo phương thẳng đứng trùng với trục của lò xo và khi vật đạt độ cao cực đại, lò xo dãn 5 cm. Lấy gia tốc trọng trường g = 10 m/s2. Vận tốc cực đại của vật dao động là
A. 0,5 m / s .
B. 1,75 m / s .
C. 2,25 m / s .
D. 3,75 m/s.
Hiển thị đáp án
Đáp án: A
Giải thích : Độ dãn của lò xo khi ở vị trí cân đối :
Δl0 = mgk = 10 ω2
Khi ở độ cao cực lớn, độ dãn của lò xo :
Δlmin = Δl0 − A ⇒ 0,05 = 10 ω2 − A
⇒ 1 ω2 = 0,1 A + 0,005
→ A2 = x02 + v02ω2A2 = 0,032 + 0,420,1 A + 0,005
⇒ A = 0,05 mA = − 0,034 m
ω = 10,1 A + 0,005 = 10 rad / s ⇒ vmax = ωA = 0,5 m / s
Câu 23. Một con lắc lò xo treo thẳng đứng có độ cứng 100 N/m, vật dao động có khối lượng 100 g, lấy gia tốc trường g = π2 = 10m/s2. Từ vị trí cân bằng kéo vật xuống một đoạn 1 cm rồi truyền cho vật vận tốc đầu 10π3cm/s hướng thẳng đứng thì vật dao động điều hòa. Thời gian lò xo bị nén trong một chu kỳ là
A. 12 s .
B. 16 s .
C. 112 s .
D. 115 s .
Hiển thị đáp án
Đáp án: D
Giải thích : Ta có :
ω = 2 πT = 10 πrad / s
A = x2 + v2ω2 = 2 cm
Chiều dài tự nhiên của lò xo là :
Δl0 = mgk = 0,01 m = 1 cm = A2
Trong 1 chu kì thời hạn lò xo nén :
tnen = 2. T6 = 13.2 πω = 115 ( s )
Câu 24. Một con lắc lò xo, gồm lò xo nhẹ có độ cứng 50 N/m, vật có khối lượng 2 kg, dao động điều hoà dọc theo trục Ox theo phương ngang (O là vị trí cân bằng) theo phương trình x=6cosωt+π3 (cm). Tính lực đàn hồi lò xo ở thời điểm t=0,4π s.
A. 1 N .
B. 1,5 N .
C. 1,75 N .
D. 2 N .
Hiển thị đáp án
Đáp án: B
Giải thích : Ta có : ω = km = 5 rad / s
⇒ x0, 4 π = 6 cos5. 0,4 π + π3 = 3 cm = 0,03 m
Fd = Fhp = kx = 50.0,03 = 1,5 N
Câu 25. Một con lắc lò xo dao động điều hòa theo phương ngang với năng lượng dao động 1J và lực đàn hồi cực đại là 10N. Gọi J là đầu cố định của lò xo. Khoảng thời gian ngắn nhất giữa hai lần liên tiếp điểm J chịu tác dụng của lực kéo 53N là 0,1s. Tính quãng đường lớn nhất mà vật đi được trong 0,7s.
A. 30 cm .
B. 50 cm .
C. 100 cm .
D. 120 cm .
Hiển thị đáp án
Đáp án: C
Giải thích : W = kA22 = 1F max = kA = 10 ⇒ A = 0,2 m = 20 cm
Do con lắc lò xo nằm ngang nên Fhp = − kx
⇒ x1A = F1Fmax ⇒ x1 = A32 ⇒ t2 = T12
Trong 1 chu kỳ luân hồi thời hạn lực kéo lớn hơn 1N là 0,1 = 2 t2 = T6 ⇒ T = 0,6 s
⇒ t = 0,7 s = 7T6 = 2T2 ⎵ 2.2 A + T6 ⎵ Smax = ASmax = 5A = 100 cm

Câu 26. Một con lắc lò xo treo thẳng đứng, m = 100 g, x=4cos10t–2π3 cm(chiều dương hướng lên). Tìm Fđh và Fhp tại thời điểm vật đó đi được quãng đường 3 cm?
A. Fdh = 0,9 N và Fhp = 0,1 N .
B. Fdh = 0,5 N và Fhp = 0,01 N .
C. Fdh = 0,09 N và Fhp = 0,01 N .
D. Fdh = 1 N và Fhp = 0,001 N .
Hiển thị đáp án
Đáp án: A
Giải thích :
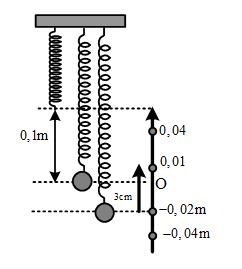
Độ cứng của lò xo và độ dãn của lò xo ở VTCB :
k = mω2 = 10N / mΔl0 = mgk = 0,1 m
Lúc đầu : x = 4 cos10t − 2 π3 = − 2 cmv = x ‘ = − 40 sin10t − 2 π3 = 203 cm / s > 0
Sau khi đi được quãng đường 3 cm thì lúc này vật có li độ x = 1 cm và độ dãn của lò xo là Δl = 0,1 − 0,01 = 0,09 m .
Độ lớn lực đàn hồi và lực hồi sinh :
Fdh = kΔl = 10.0,09 = 0,9 NFhp = kx = 10.0,01 = 0,1 N
Câu 27. Một con lắc lò xo treo thẳng đứng vào điểm J tại nơi có gia tốc rơi tự do 10 (m/s2). Khi vật dao động điều hòa thì lực nén cực đại lên điểm treo J là 2 N còn lực kéo cực đại lên điểm treo J là 4 N. Gia tốc cực đại của vật dao động là:
A. 20 m / s2 .
B. 30 m / s2 .
C. 15 m / s2 .
D. 25 m / s2 .
Hiển thị đáp án
Đáp án: B
Giải thích : Lực kéo cực lớn : Fkeo_max = kΔl0 + A = 4N ;
Lực nén cực lớn : Fnen_max = kA − Δl0 = 2N
⇒ A = 3 kΔl0 = 1 k ⇒ amax = ω2A = kmA = gΔl0A = 30 m / s2
Câu 28. Một con lắc lò xo treo thẳng đứng dao động điều hòa với biên độ A. Trong quá trình dao động, chiều dài lớn nhất và nhỏ nhất của lò xo là 34 cm và 20 cm, tỉ số lực đàn hồi lớn nhất và nhỏ nhất của lò xo là 103. Lấy g=π2=10m/s2. Tính chiều dài tự nhiên của lò xo.
A. 10 cm .
B. 12 cm .
C. 14 cm .
D. 18 cm .
Hiển thị đáp án
Đáp án: C
Giải thích : Ta có :
FmaxFmin = kΔl0 + AkΔl0 − A = l0 + Δl0 + A − l0l0 + Δl0 − A − l0 = lmax − l0lmin − l0
⇒ 103 = 34 − l020 − l0 ⇒ l0 = 14 cm
Câu 29. Một con lắc lò xo đặt trên mặt phẳng nằm ngang gồm lò xo nhẹ có một đầu cố định, đầu kia gắn với vật nhỏ m1. Ban đầu giữ vật m1 tại vị trí mà lò xo bị nén 8 cm, đặt vật nhỏ m2 (m2 = m1) trên mặt phẳng nằm ngang và sát với vật m1. Buông nhẹ để hai vật bắt đầu chuyển động theo phương của trục lò xo. Bỏ qua mọi ma sát. Ở thời điểm lò xo có chiều dài cực đại lần đầu tiên thì khoảng cách giữa hai vật m1 và m2 là
A. 2.1 cm .
B. 3,2 cm .
C. 5,5 cm .
D. 7,1 cm .
Hiển thị đáp án
Đáp án: B
Giải thích: – Giai đoạn 1: Cả hai vật cùng dao động với biên độ A,
tần số góc ω = km1 + mét vuông, vận tốc cực lớn v0 = ωA .
– Giai đoạn 2: Đến VTCB m2 tách khỏi m1 thì:
+ m1 giao động điều hòa với tần số góc ω ‘ = km1
và biên độ A ‘ = v0ω ‘ = Am1m1 + mét vuông
( vì vận tốc cực lớn không đổi vẫn là v0 ) .
+ mét vuông hoạt động thẳng đều với tốc độ v0 và khi m1 đến vị trí biên dương ( lần 1 ) thì mét vuông đi được quãng đường
S = v0T ‘ 4 = km1 + m2A. 142 πm1k = π2Am1m1 + mét vuông
Lúc này khoảng cách giữa hai vật :
Δx = S − A ‘ = πA2m1m1 + mét vuông − Am1m1 + mét vuông ≈ 3,2 cm
Câu 30. Một con lắc lò xo có độ cứng k = 100N/m và vật nặng khối lượng m=59 kg đang dao động điều hòa với biên độ A = 2,0 cm trên mặt phẳng nằm ngang nhẵn. Tại thời điểm vật m qua vị trí mà động năng bằng thế năng, một vật nhỏ khối lượng m0=m2 rơi thẳng đứng và dính vào m. Khi qua vị trí cân bằng hệ (m + m0) có tốc độ
A. 10 cm / s .
B. 20 cm / s .
C. 30 cm / s .
D. 40 cm / s .
Hiển thị đáp án
Đáp án: B
Giải thích : Li độ và vận tốc của m ngay trước lúc va chạm :
x1 = A2 = 2 cmv1 = ωA2 = 610 cm / s
Tốc độ của con lắc ngay sau va chạm :
V1 = mv1m + m0 = 410 cm / s
Cơ năng của con lắc sau đó :
W ‘ = m + m0vmax22 = kx122 + m + m0V122
⇒ vmax = 20 cm / s
Câu 31. Con lắc lò xo treo thẳng đứng. Nâng vật lên đến vị trí lò xo không biến dạng và thả không vận tốc ban đầu thì vật dao động điều hòa theo phương thẳng đứng trùng với trục của lò xo, khi vận tốc của vật là 1 m/s thì gia tốc của vật là 5 m/s2. Lấy gia tốc trọng trường 10 m/s2. Tần số góc có giá trị là:
A. 2 rad / s .
B. 3 rad / s .
C. 4 rad / s .
D. 5 √ 3 rad / s .
Hiển thị đáp án
Đáp án: D
Giải thích :
– Vì đưa vật lên đến độ cao lúc không bị biến dạng nên biên độ A = Δl .
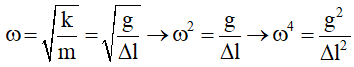
– Áp dụng công thức độc lập của v và a ta có :
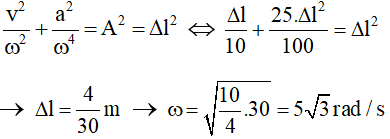
Câu 32. Cho một lò xo có chiều dài tự nhiên OA = 50 cm, độ cứng 20 N/m. Treo lò xo OA thẳng đứng, O cố định. Móc quả nặng m = 1 kg vào điểm C của lò xo. Cho quả nặng dao động theo phương thẳng đứng. Biết chu kì dao động của con lắc là 0,628 s. Điểm C cách điểm O một khoảng bằng:
A. 20 cm .
B. 7,5 cm .
C. 15 cm .
D. 10 cm .
Hiển thị đáp án
Đáp án: D
Giải thích :
– Ta có :
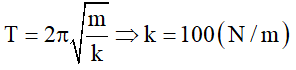
– Lò xo lí tưởng nên :
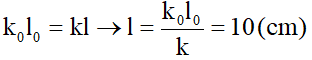
– Lúc lò xo chưa treo vật thì :
OC = l = 10 cm
– Vậy điểm C cách điểm O một khoảng chừng bằng 10 cm .
Câu 33. Một con lắc lò xo gồm lò xo nhẹ có độ cứng 100 N/m và vật nhỏ khối lượng m. Con lắc dao động điều hòa theo phương ngang với chu kì T. Biết ở thời điểm t vật có li độ 5 cm, ở thời điểm t + T/4 vật có tốc độ 50 cm/s. Giá trị của m bằng:
A. 0,5 kg .
B. 1,2 kg .
C. 0,8 kg .
D. 1,0 kg .
Hiển thị đáp án
Đáp án: D
Giải thích :
– Từ thời gian t đến thời gian t + T / 4 thì góc quay thêm là : Δφ + π / 2
– Ở thời gian t + T / 4 :
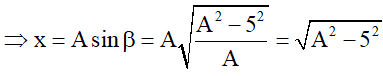
luôn có :
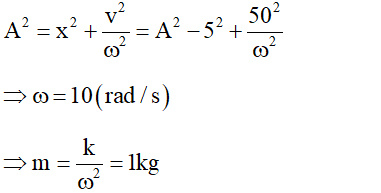
Câu 34. Con lắc lò xo gồm vật nhỏ gắn với lò xo nhẹ dao động điều hòa theo phương ngang. Lực kéo về tác dụng vào vật luôn:
A. cùng chiều với chiều hoạt động của vật .
B. hướng về vị trí biên .
C. cùng chiều với chiều biến dạng của lò xo .
D. hướng về vị trí cân đối .
Hiển thị đáp án
Đáp án: D
Giải thích :
– Lực kéo về công dụng lên vật luôn hướng về vị trí cân đối .
Câu 35. Một con lắc lò xo gồm vật nhỏ khối lượng 0,02 kg và lò xo có độ cứng 1 N/m. Vật nhỏ được đặt trên giá đỡ cố định nằm ngang dọc theo trục lò xo. Hệ số ma sát trượt giữa giá đỡ và vật nhỏ là 0,1. Ban đầu giữ vật ở vị trí lò xo bị nén 10 cm rồi buông nhẹ để con lắc dao động tắt dần. Lấy g = 10 m/s2. Tốc độ lớn nhất vật nhỏ đạt được trong quá trình dao động là:
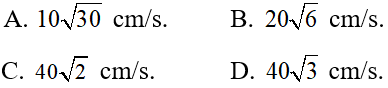
Hiển thị đáp án
Đáp án: C
Giải thích :
– Biên độ giao động : A = 10 cm
– Tần số góc: 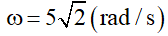
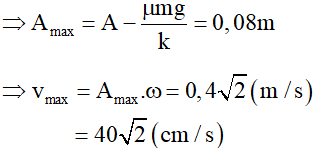
Câu 36. Một con lắc lò xo dao động điều hòa theo trục x nằm ngang. Lò xo có độ cứng k = 100 N/m. Khi vật có khối lượng m của con lắc đi qua vị trí có li độ x = 4 cm theo chiều âm thì thế năng của con lắc đó là bao nhiêu?
A. 8 J .
B. 0,08 J .
C. – 0,08 J .
D. – 8 J .
Hiển thị đáp án
Đáp án: B
Giải thích :
– Thế năng của con lắc lò xo là :
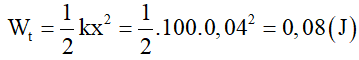
Câu 37. Một con lắc lò xo gồm một vật nhỏ và lò xo nhẹ có độ cứng 100 N/m. Con lắc dao động đều hòa theo phương ngang với phương trình x = Acos(ωt + φ). Mốc thế năng tại vị trí cân bằng. Khoảng thời gian giữa hai lần liên tiếp con lắc có động năng bằng thế năng là 0,1 s. Lấy π2 = 10. Khối lượng vật nhỏ bằng
A. 400 g .
B. 40 g .
C. 200 g .
D. 100 g .
Hiển thị đáp án
Đáp án: A
Giải thích :
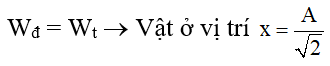
– Khoảng thời hạn giữa 2 lần liên tục Wđ = Wt là :
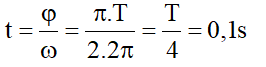
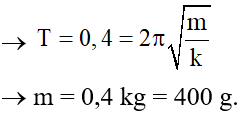
Câu 38. Một con lắc lò xo đang dao động điều hòa với biên độ 5 cm và chu kì 0,5 s trên mặt phẳng nằm ngang. Khi vật nhỏ của con lắc có tốc độ v thì người ta giữ chặt một điểm trên lò xo, vật tiếp tục dao động điều hòa với biên độ 2,25 cm và chu kì 0,25 s. Giá trị của v gần nhất với giá trị nào sau đây?
A. 50 cm / s .
B. 60 cm / s .
C. 70 cm / s .
D. 40 cm / s .
Hiển thị đáp án
Đáp án: A
Giải thích :
– Tại thời gian giữ, lò xo dãn 1 đoạn Δl0, khi đó phần lò xo không tham gia vào quy trình giao động sau khi giữ có độ dãn Δl .
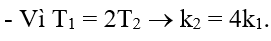
– Phần lò xo không tham gia vào quy trình xê dịch sau khi giữ là :
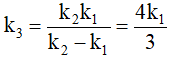
– Ta xem như lò xo bị cắt nên :
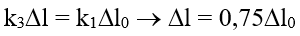
– Áp dụng định luật bảo toàn nguồn năng lượng ta có :
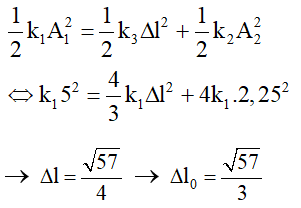
– Áp dụng công thức độc lập ta có :
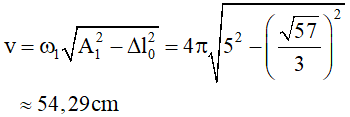
⇒ Gần với giá trị của đáp án A nhất .
Câu 39. Một con lắc lò xo đang dao động điều hòa với chu kì T, vật dao động có khối lượng m. Độ cứng lò xo là:
A. 2 π2m / T2 .
B. 0,25 mT2 / π2 .
C. 4 π2m / T2 .
D. 4 π2m / T .
Hiển thị đáp án
Đáp án: A
Giải thích :
– Ta có :
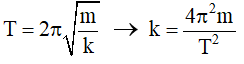
Câu 40. Một con lắc lò xo treo thẳng đứng vào điểm J tại nơi có gia tốc rơi tự do 10 (m/s2). Khi vật dao động điều hòa thì lực nén cực đại lên điểm treo J là 2 N còn lực kéo cực đại lên điểm treo J là 4 N. Gia tốc cực đại của vật dao động là:

Hiển thị đáp án
Đáp án: D
Giải thích :
– Ta có :
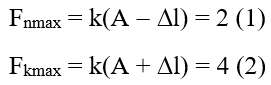
– Lập tỉ số ( 1 ) và ( 2 ) ta được : A = 3 Δl
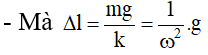
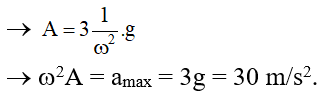
Các câu hỏi trắc nghiệm Vật lí lớp 12 có đáp án, chọn lọc khác:
Trắc nghiệm Con lắc đơn có đáp án
Trắc nghiệm Dao động tắt dần. Dao động cưỡng bức có đáp án
Trắc nghiệm Tổng hợp hai giao động điều hòa cùng phương, cùng tần số. Phương pháp Fre-nen có đáp án
Trắc nghiệm Sóng cơ và sự truyền sóng cơ có đáp án