Các lò xo thường có một vị trí cân đối khi ” nghỉ ” ( không có ngoại lực tác động ảnh hưởng ), nhưng cũng có lò xo có nhiều vị trí nghỉ. Lò xo trên kim chỉ nan chuyển hóa hàng loạt công suất của ngoại lực khi tác động ảnh hưởng thành thế năng đàn hồi, và giải phóng hàng loạt thế năng này trở lại thành công cơ học khi không có ngoại lực. Thực tế, không có lò xo như vậy. Lò xo thực tiễn luôn tiêu tốn một phần công suất ngoại lực thành nhiệt năng hay nguồn năng lượng khác không hồi sinh được .
Lò xo đầu tiên được loài người phát minh là cung tên, một mảnh gỗ cong và đàn hồi, có tác dụng dự trữ năng lượng khi uốn cong bằng tay và giải phóng năng lượng này thành động năng của mũi tên. Các bức vẽ cổ cho biết cung tên đã được sử dụng từ cách đây 10000 năm.
lò xo lá( thấy trong chuột máy tính dây rút)- lò xo theo trục( kiểu thường ta vẫn thấy)
Kẹp quần áo có lò xo
Ngày nay, lò xo được ứng dụng thoáng rộng. Một số ví dụ như :
Liên hệ lực đàn hồi theo biến dạng[sửa|sửa mã nguồn]
Đa số lò xo tuân theo liên hệ tuyến tính giữa lực đàn hồi và biến dạng (định luật Hooke). Hệ số đàn hồi, hay độ cứng, của lò xo được định nghĩa là hằng số k:
-
k
=
F
x
{\displaystyle k={\frac {F}{x}}}
k = T θ { \ displaystyle k = { \ frac { T } { \ theta } } }
Với F hay T là lực (với lò xo kéo/nén) hay mômen lực (với lò xo quay); x hay
θ
{\displaystyle \theta }
là độ co giãn hay góc quay. Nghịch đảo độ cứng, 1/k, là độ dẻo.
Lực của lò xo luôn ngược hướng với chiều biến dạng. Tức là lực lò xo luôn có xu hướng làm vật trở về trạng thái không biến dạng. Do dó, lực lò xo còn gọi là lực hồi phục, giúp vật trở lại vị trí cân bằng, luôn hướng về vị trí cân bằng. Có thể thể hiện hướng của lực lò xo:
- F = –kx
với x là độ rời khỏi vị trí cân bằng, k là hệ số đàn hồi hay độ cứng của lò xo.
Thực tế nhiều ứng dụng yên cầu những lò xo có liên hệ giữa lực và biến dạng không tuyến tính. Bảng dưới tóm tắt những trường hợp cơ bản .
Tuyến tính
Các lò xo có đặc tính gần với định luật Hooke nhất là các lò xo xoắn ốc với rất nhiều vòng xoắn, dùng trong các thiết bị đo hay trong đồng hồ.
|
|
|
Gần tuyến tính
Đây là các lò xo thông dụng trong công nghiệp, tuân thủ gần đúng định luật Hooke ở những biến dạng nhỏ hay trên các đoạn nhỏ chứ không trên toàn bộ lò xo. Các lò xo sản xuất đại trà, dù cùng lô sản xuất, cũng có thể có tính chất thay đổi mạnh từ cái này đến cái kia, với độ cứng có thể thay đổi đến 20%.
|
|
|
Tuyến tính lệch
Để làm biến dạng loại lò xo này, lực tác động cần vượt qua một ngưỡng nhất định. Sau ngưỡng đó, biến dạng là gần tuyến tính với lực.
|
|
|
Phi tuyến dương tính
Đối với dạng này, biến dạng lớn đòi hỏi lực lớn hơn là quan hệ tuyến tính.
|
|
 
|
Trung tính hay Âm tính
Các lò xo kiểu này có thể là tấm sắt bị hút bởi nam châm. Trong trường lực của nam châm, khi tấm sắt bị đẩy ra xa, lực hút giảm.
|
|
|
Biến đổi
Loại lò xo này có thể được ứng dụng trong các phím bấm. Chúng tạo nên các tín hiệu bấm chính xác, và cảm giác giác sử dụng thuận tiện.
|
|
|
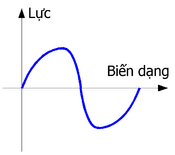
Không hồi phục
Loại lò xo này giữ nhiều trạng thái nghỉ, và chuyển từ trạng thái này sang trạng thái kia khi biến dạng vượt qua một giới hạn nhất định. Trong giới hạn, biến dạng vẫn có thể hồi phục.
|
|
|
Liên kết ngoài[sửa|
Một lò xo
