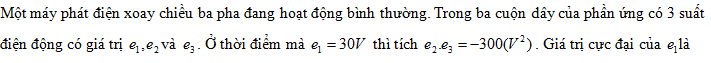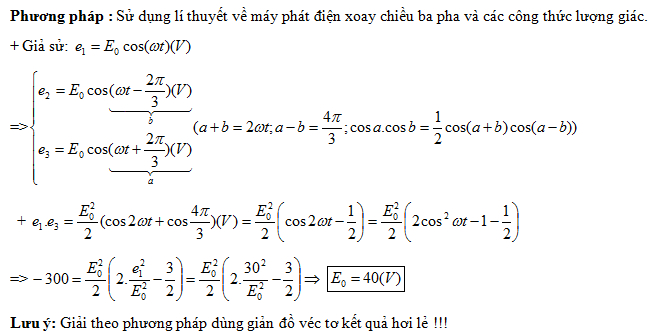50 bài tập Máy phát điện xoay chiều mức độ vận dụng

Câu hỏi 1 :Hai máy phát điện xoay chiều một pha A và B ( có phần cảm là rôto ) đang hoạt động giải trí không thay đổi, phát ra hai suất điện động có cùng tần số 60 Hz. Biết phần cảm của máy A nhiều hơn phần cảm của máy B 2 cặp cực ( 2 cực bắc, 2 cực nam ) và trong 1 giờ số vòng xoay của rôto hai máy chênh lệch nhau 18000 vòng. Số cặp cực của máy A và máy B lần lượt là

• A4 và 2.

• B

  Bạn đang đọc: 50 bài tập Máy phát điện xoay chiều mức độ vận dụng

  5 và 3.

• C6 và 4.
• D8 và 6.

Đáp án: C

Lời giải chi tiết cụ thể :

Đáp án – Lời giải Câu hỏi 2 :Máy phát điện xoay chiều một pha thứ nhất có 2 p cặp cực từ, roto quay với vận tốc n vòng / phút thì phát ra suất điện động có tần số 60 Hz. Máy phát điện xoay chiều một pha thứ hai có p / 2 cặp cực từ, roto quay với vận tốc lớn hơn của máy thứ nhất 525 vòng / phút thì tần số của suất điện động do máy phát ra là 50 Hz. Số cặp cực từ của máy thứ 2 bằng :

• A8
• B6
• C4
• D16

Đáp án: C

Phương pháp giải :Công thức tính tần số : f = np ( n ( vòng / s ) là vận tốc quay của roto ; p là số cặp cực )Lời giải chi tiết cụ thể :Ta có :

\(\left\{ \matrix{
60 = {{2pn} \over {60}} \hfill \cr
50 = {{{p \over 2}.(n + 525)} \over {60}} \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
60 = {{2pn} \over {60}} \Rightarrow np = 1800 \hfill \cr
50 = {{{p \over 2}.(n + 525)} \over {60}} \Leftrightarrow 3000 = {{np} \over 2} + {{525p} \over 2} \hfill \cr} \right. \Rightarrow 3000 = {{1800} \over 2} + {{525p} \over 2} \Rightarrow p = 8\)

=> Số cặp cực từ của máy thứ 2 là : p / 2 = 4
Chọn CĐáp án – Lời giải Câu hỏi 3 :

Hai đầu ra của máy phát điện xoay chiều 1 pha đuọc nối với một đoạn mạch nối tiếp gồm tụ điện và điện trở thuần. Bỏ qua điện trở thuần của các cuộn dây của máy phát. Khi roto quay với tốc độ 600 vòng/phút thì cường độ dòng điện trong mạch là I1 ≈ 3,16A. Khi roto quay với tốc độ 1200 vòng/phút thì cường độ dòng điện trong mạch là I2 = 8A. Khi roto quay với tốc độ 1800 vòng/phút thì cường độ dòng điện hiệu dụng gần nhất với giá trị nào sau đây?

• A12,5 A
• B13,5A
• C10,5A
• D11,5A

Đáp án: A

Phương pháp giải :Chuẩn hóa số liệuLời giải cụ thể :

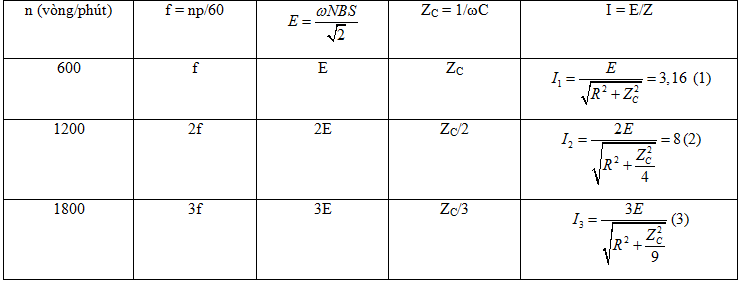
Từ ( 1 ), ( 2 ) và ( 3 ) => I3 = 12,7 A
Chọn AĐáp án – Lời giải Câu hỏi 4 :Hai máy phát điện xoay chiều một pha phát ra dòng điện xoay chiều có cùng tần số f. Máy thứ nhất có p cặp cực, quay với vận tốc 27 vòng / phút, máy thứ hai có 4 cặp cực, quay với vận tốc n vòng / phút ( với \ ( 10 \ le n \ le \ ) 20 ). Giá trị của f là

• A50Hz
• B54Hz
• C64Hz
• D60Hz

Đáp án: B

Phương pháp giải :Tần số dòng điện : f = np ( n có đơn vị chức năng là vòng / phút )Lời giải chi tiết cụ thể :

Tần số dòng điện: \(f = p.27 = 4n;10 \le n \le 20 \to 1,48 \le p \le 2,96 \Rightarrow p = 2 \Rightarrow f = 54Hz\)

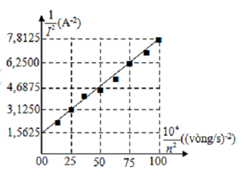
Đáp án – Lời giải Câu hỏi 5 :Nối hai cực của máy phát điện xoay chiều một pha vào hai đầu một cuộn dây không thuần cảm có điện trở r = 10 π W và độ tự cảm L. Biết rôto của máy phát có một cặp cực, stato của máy phát có 20 vòng dây và điện trở thuần của cuộn dây là không đáng kể. Cường độ dòng điện trong mạch được đo bằng đồng hồ đeo tay đo điện đa năng hiện số. Kết quả thực nghiệm thu được như đồ thị trên hình vẽ. Giá trị của L là

• A0,25 H.
• B0,30 H.
• C0,20 H.
• D0,35 H

Đáp án: A

Phương pháp giải :Suất điện động hiệu dụng E = ωϕ
Cường độ dòng điện hiệu dụng I = E / Z
Tần số của dòng điện xoay chiều f = np ( n là vận tốc quay của roto ; p là số cặp cực )Lời giải cụ thể :Ta có : \ ( I = { { \ omega \ Phi } \ over { \ sqrt { { r ^ 2 } + { \ omega ^ 2 } { L ^ 2 } } } } \ Rightarrow { 1 \ over { { I ^ 2 } } } = { { { r ^ 2 } } \ over { { \ omega ^ 2 } { \ Phi ^ 2 } } } + { { { L ^ 2 } } \ over { { \ Phi ^ 2 } } } \ )
Có : f = np ; p = 1 => ω = 2 πn ; r = 10 π ( Ω ) \ ( \ Rightarrow { 1 \ over { { I ^ 2 } } } = { { { r ^ 2 } } \ over { 4 { \ pi ^ 2 } { n ^ 2 } { \ Phi ^ 2 } } } + { { { L ^ 2 } } \ over { { \ Phi ^ 2 } } } \ )
+ \ ( { { { { 10 } ^ 4 } } \ over { { n ^ 2 } } } = 0 \ Rightarrow { 1 \ over { { n ^ 2 } } } = 0 \ Rightarrow { 1 \ over { I_0 ^ 2 } } = { { { L ^ 4 } } \ over { { \ Phi ^ 2 } } } = 1,5625 \ ) ( 1 )
+ \ ( { { { { 10 } ^ 4 } } \ over { { n ^ 2 } } } = 100 \ Rightarrow { 1 \ over { { n ^ 2 } } } = 0,01 \ Rightarrow { 1 \ over { { I ^ 2 } } } = { { { r ^ 2 } } \ over { 100.4 { \ pi ^ 2 } { \ Phi ^ 2 } } } + { { { L ^ 2 } } \ over { { \ Phi ^ 2 } } } = 7,8125 \ ) ( 2 )
+ \ ( { { ( 1 ) } \ over { ( 2 ) } } = { { { L ^ 2 } } \ over { { { { r ^ 2 } } \ over { 100.4 { \ pi ^ 2 } } } + { L ^ 2 } } } = { { 1,5625 } \ over { 7,8125 } } = { 1 \ over 5 } \ Rightarrow L = 0,25 H \ )Đáp án – Lời giải Câu hỏi 6 :Một xí nghiệp sản xuất phát điện gồm n tổ máy, mỗi tổ máy có cùng hiệu suất P. Điện sản xuất ra được truyền đến nơi tiêu thụ với hiệu suất H. Hỏi nếu khi chỉ còn một tổ máy thì hiệu suất H ’ bằng bao nhiêu ( tính theo n và H )

• A\(H’ = {H \over n}\)
• BH’ = H
• C\(H’ = {{n + H – 1} \over n}\)
• DH’= nH

Đáp án: C

Phương pháp giải :vận dụng công thức tính hiệu suất truyền tải trong truyền tải điện năng đi xa .Lời giải cụ thể :

Đáp án C

+ Hiệu suất truyền tải ứng với n tổ máy \ ( H = 1 – { { nP } \ over { { U ^ 2 } } } R \ )
+ Hiệu suất truyền tải ứng với n tổ máy \ ( H ‘ = 1 – { P \ over { { U ^ 2 } } } R \ )
\ ( \ to H ‘ = { { n – 1 + H } \ over n } \ )
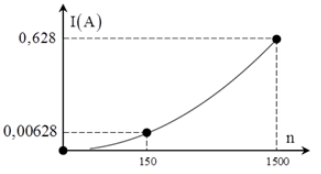
Đáp án – Lời giải Câu hỏi 7 :Rô to của một máy phát điện xoay chiều một pha có 4 cực từ và quay với vận tốc n vòng / phút. Hai cực phần ứng của máy mắc với một tụ điện có điện dung C = 10 μF. Điện trở trong của máy không đáng kể. Đồ thị trình diễn sự biến thiên của cường độ dòng điện hiệu dụng I qua tụ theo vận tốc quay của rô to khi vận tốc quay của rô to biến thiên liên tục từ n1 = 150 vòng / phút đến n2 = 1500 vòng / phút. Biết rằng với vận tốc quay 1500 vòng / phút thì suất điện động hiệu dụng giữa hai cực máy phát tương ứng là E. Giá trị E là

• A400 V.
• B100 V. 
• C 200 V.
• D 300 V.

Đáp án: B

Lời giải chi tiết cụ thể :

Đáp án B

+ Ta có \ ( E = I { Z_C } = { I \ over { C2 \ pi f } } = { { 0,628 } \ over { { { 10.10 } ^ { – 6 } }. 2 \ pi. { { 4.1500 } \ over { 60 } } } } = 100 \, \, V. \ )Đáp án – Lời giải Câu hỏi 8 :

Nối hai cực của một máy phát điện xoay chiều một pha vào hai đầu đoạn mạch AB gồm điện trở thuần \(R = 100\sqrt 2 \Omega \), cuộn cảm thuần L = 5/3π H và tụ điện \(C = {{{{5.10}^{ – 4}}} \over {6\pi }}F\) mắc nối tiếp. Bỏ qua điện trở các cuộn dây của máy phát điện và điện trở dây nối. Máy phát điện có số cặp cực không đổi, tốc độ quay của roto thay đổi được. Khi tốc độ quay của roto bằng n (vòng/phút) thì công suất của mạch đạt giá trị lớn nhất bằng 161,5W. Khi tốc độ quay của roto bằng 2n (vòng/phút) thì công suất tiêu thụ của mạch là:

• A136W
• B126W
• C148W
• D125W

Đáp án: A

Phương pháp giải :Công thức tính hiệu suất tiêu thụ của mạch : \ ( P = { { { U ^ 2 } R } \ over { { Z ^ 2 } } } = { { { { \ left ( { { { \ omega { \ Phi _0 } } \ over { \ sqrt 2 } } } \ right ) } ^ 2 }. R } \ over { { R ^ 2 } + { { \ left ( { { Z_L } – { Z_C } } \ right ) } ^ 2 } } } = { { { \ omega ^ 2 } { \ Phi ^ 2 }. R } \ over { { R ^ 2 } + { { \ left ( { { Z_L } – { Z_C } } \ right ) } ^ 2 } } } \ )Lời giải chi tiết cụ thể :

+ Khi vận tốc quay của roto là n ( vòng / phút ) :

\(\eqalign{
& P = {{{\omega ^2}{\Phi ^2}.R} \over {{R^2} + {{\left( {{Z_L} – {Z_C}} \right)}^2}}} = {{{\omega ^2}{\Phi ^2}.R} \over {{R^2} + {{\left( {\omega L – {1 \over {\omega C}}} \right)}^2}}} = {{{\omega ^2}{\Phi ^2}.R} \over {{R^2} + {\omega ^2}{L^2} – {{2L} \over C} + {1 \over {{\omega ^2}{C^2}}}}} = {{{\Phi ^2}.R} \over {{{{R^2}} \over {{\omega ^2}}} + {L^2} – {{2L} \over {{\omega ^2}C}} + {1 \over {{\omega ^4}{C^2}}}}} \cr
& \Rightarrow P = {{{\Phi ^2}.R} \over {{1 \over {{\omega ^4}{C^2}}} + \left( {{R^2} – {{2L} \over C}} \right){1 \over {{\omega ^2}}} + {L^2}}} \cr} \)

\(\eqalign{
& {P_{\max }} \Leftrightarrow {\left[ {{1 \over {{\omega ^4}{C^2}}} + \left( {{R^2} – {{2L} \over C}} \right){1 \over {{\omega ^2}}} + {L^2}} \right]_{\min }} \Leftrightarrow {1 \over {{\omega ^2}}} = {{{{2L} \over C} – {R^2}} \over {{2 \over {{C^2}}}}} = {{2{5 \over {3\pi }}.{{6\pi } \over {{{5.10}^{ – 4}}}} – {{\left( {100\sqrt 2 } \right)}^2}} \over {{2 \over {{{\left( {{{6\pi } \over {{{5.10}^{ – 4}}}}} \right)}^2}}}}} = {1 \over {14400{\pi ^2}}} \Rightarrow \omega = 120\pi \cr
& \Rightarrow \left\{ \matrix{
{Z_L} = \omega L = 120\pi .{5 \over {3\pi }} = 200\Omega \hfill \cr
{Z_C} = {1 \over {\omega C}} = {1 \over {120\pi .{{{{5.10}^{ – 4}}} \over {6\pi }}}} = 100\Omega \hfill \cr} \right. \Rightarrow {P_{m{\rm{ax}}}} = {{{\omega ^2}{\Phi ^2}R} \over {{R^2} + {{\left( {200 – 100} \right)}^2}}} = 161,5(*) \cr} \)

+ Khi tốc độ quay của roto là 2n (vòng/phút)

\( \Rightarrow \left\{ \matrix{
{Z_L}’ = 2{Z_L} = 400\Omega \hfill \cr
{Z_C}’ = {{{Z_C}} \over 2} = 50\Omega \hfill \cr} \right. \Rightarrow P’ = {{\omega {‘^2}{\Phi ^2}R} \over {{R^2} + {{\left( {{Z_L}’ – {Z_C}’} \right)}^2}}} = {{4{\omega ^2}R} \over {{R^2} + {{\left( {400 – 50} \right)}^2}}}(**)\)

Từ ( * ) và ( * * ) \ ( \ Rightarrow { { P ‘ } \ over { { P_ { m { \ rm { ax } } } } } } = { { \ omega { ‘ ^ 2 } } \ over { { \ omega ^ 2 } } }. { { { R ^ 2 } + { { \ left ( { 200 – 100 } \ right ) } ^ 2 } } \ over { { R ^ 2 } + { { \ left ( { 400 – 50 } \ right ) } ^ 2 } } } \ Leftrightarrow { { P ‘ } \ over { 161,5 } } = 4. { { { { \ left ( { 100 \ sqrt 2 } \ right ) } ^ 2 } + { { 100 } ^ 2 } } \ over { { { \ left ( { 100 \ sqrt 2 } \ right ) } ^ 2 } + { { 350 } ^ 2 } } } = { { 16 } \ over { 19 } } \ Rightarrow P ‘ = 136W \ )Đáp án – Lời giải Câu hỏi 9 :

Một máy phát điện xoay chiều một pha có điện trở không đáng kể,được mắc với mạch ngoài là một đoạn mạch mắc nối tiếp gồm điện thuần R, cuộn cảm thuần L và tụ điện C. Khi tốc độ quay của lần lượt 360 vòng/ phút  và 800 vòng /phút thì cường độ dòng điện hiệu dụng trong mạch là như nhau. Khi tốc độ quay là n0­ thì cường độ hiệu dụng trong mạch đạt cực đại. n0  có giá trị gần với giá trị nào sau đây ?

• A620 vòng/ phút
• B537 vòng / phút
• C464 vòng /phút
• D877 vòng /phút

Đáp án: C

Phương pháp giải :Tần số của dòng điện f = np ( n là vận tốc quay của roto, p là số cặp cực )
Sử dụng lí thuyết về mạch điện xoay chiều có f biến hóa .Lời giải chi tiết cụ thể :Suất điện động của nguồn điện : \ ( E = { { \ omega N { \ Phi _0 } } \ over { \ sqrt 2 } } = { { 2 \ pi fN { \ Phi _0 } } \ over { \ sqrt 2 } } = U \ ) ( do r = 0 )
Với f = np ( n vận tốc quay của roto, p số cặp cực từ )
Do I1 = I2 ta có :

\(\eqalign{
& {{\omega _1^2} \over {{R^2} + {{({\omega _1}L – {1 \over {{\omega _1}C}})}^2}}} = {{\omega _2^2} \over {{R^2} + {{({\omega _2}L – {1 \over {{\omega _2}C}})}^2}}} \Rightarrow \omega _1^2[{R^2} + {({\omega _2}L – {1 \over {{\omega _2}C}})^2}] = \omega _2^2[{R^2} + {({\omega _1}L – {1 \over {{\omega _1}C}})^2}] \cr
& \Rightarrow \omega _1^2{R^2} + \omega _1^2\omega _2^2{L^2} + {{\omega _1^2} \over {\omega _2^2{C^2}}} – 2\omega _1^2{L \over C} = \omega _2^2{R^2} + \omega _1^2\omega _2^2{L^2} + {{\omega _2^2} \over {\omega _1^2{C^2}}} – 2\omega _2^2{L \over C} \cr
& \Rightarrow (\omega _1^2 – \omega _2^2)({R^2} – 2{L \over C}) = {1 \over {{C^2}}}({{\omega _2^2} \over {\omega _1^2}} – {{\omega _1^2} \over {\omega _2^2}}) = {1 \over {{C^2}}}{{(\omega _2^2 – \omega _1^2)(\omega _2^2 + \omega _1^2)} \over {\omega _1^2\omega _2^2}} \cr
& \Rightarrow (2{L \over C} – {\rm{ }}{R^2}){C^2} = {1 \over {\omega _1^2}} + {1 \over {\omega _2^2}}\;(*) \cr} \)

Dòng điện hiệu dụng qua mạch : \ ( I = { U \ over Z } = { E \ over Z } \ )
I = I ­ mac khi E2 / Z2 có giá trị lớn nhất hay khi \ ( y = { { \ omega _0 ^ 2 } \ over { { R ^ 2 } + { { ( { \ omega _0 } L – { 1 \ over { { \ omega _0 } C } } ) } ^ 2 } } } \ ) có giá trị lớn nhất
\ ( y = { 1 \ over { { { { R ^ 2 } + \ omega _0 ^ 2 { L ^ 2 } + { 1 \ over { \ omega _0 ^ 2 { C ^ 2 } } } – 2 { L \ over C } } \ over { \ omega _0 ^ 2 } } } } = { 1 \ over { { 1 \ over { { C ^ 2 } } } { 1 \ over { \ omega _0 ^ 4 } } + { { { R ^ 2 } – 2 { L \ over C } } \ over { \ omega _0 ^ 2 } } – { L ^ 2 } } } \ )
Để y = ymax thì mẫu số bé nhất
Đặt \ ( x = { 1 \ over { \ omega _0 ^ 2 } } \ Rightarrow y = { { { x ^ 2 } } \ over { { C ^ 2 } } } + ( { R ^ 2 } – 2 { L \ over C } ) x – { L ^ 2 } \ )
Lấy đạo hàm mẫu số, cho bằng 0 ta được hiệu quả \ ( { x_0 } = { 1 \ over { \ omega _0 ^ 2 } } = { 1 \ over 2 } { C ^ 2 } \ left ( { 2 { L \ over C } – { R ^ 2 } } \ right ) \ left ( { * * } \ right ) \ )
Từ ( * ) và ( * * ) ta suy ra : \ ( { 1 \ over { \ omega _1 ^ 2 } } + { 1 \ over { \ omega _2 ^ 2 } } = { 2 \ over { \ omega _0 ^ 2 } } \ Leftrightarrow { 1 \ over { f_1 ^ 2 } } + { 1 \ over { f_2 ^ 2 } } = { 2 \ over { f_0 ^ 2 } } \ )
hay \ ( { 1 \ over { n_1 ^ 2 } } + { 1 \ over { n_2 ^ 2 } } = { 2 \ over { n_0 ^ 2 } } \ Rightarrow n_0 ^ 2 = { { 2 n_1 ^ 2. n_2 ^ 2 } \ over { n_1 ^ 2 + n_2 ^ 2 } } = { { { { 2.360 } ^ 2 } { {. 800 } ^ 2 } } \ over { { { 360 } ^ 2 } + { { 800 } ^ 2 } } } \ Rightarrow n = 464 ( vong / phut ) \ )Đáp án – Lời giải Câu hỏi 10 :Nối hai cực của một máy phát điện xoay chiều một pha vào hai đầu đoạn mạch RLC mắc tiếp nối đuôi nhau gồm cuộn cảm thuần có độ tự cảm L = 2 / π H, tụ điện có điện dung C = 10-4 / π F, điện trở R = 100 Ω. Bỏ qua điện trở thuần của những cuộn dây máy phát. Biết rô to máy phát có hai cặp cực. Khi rô to quay đều với vận tốc n = 1500 vòng / phút thì cường độ dòng điện hiệu dụng qua mạch là \ ( \ frac { { \ sqrt 2 } } { 2 } A \ ). Khi biến hóa vận tốc quay của rô to đến giá trị n0 thì điện áp hiệu dụng trên tụ điện có giá trị cực lớn là UCmax, giá trị của n0 là UCmax lần lượt là

• A\(750\sqrt 2 \) vòng/phút; 100 V  
• B\(750\sqrt 2 \) vòng/phút;  \(50\sqrt 3 V\)
• C6000 vòng/phút; 50 V                                 
• D1500 vòng/phút; \(50\sqrt 2 V\)

Đáp án: A

Phương pháp giải :Sử dụng lí thuyết về máy phát điện xoay chiều một pha, lí thuyết về mạch điện xoay chiều mắc tiếp nối đuôi nhau và bài toán đổi khác vận tốc quay để UCmaxLời giải chi tiết cụ thể :+ Khi vận tốc quay của ddooongj cơ là 1500 vòng / phút thì tần số của dòng điện là f = pn / 60 = 50H z
Khi đó, ta tính được ZL = 200 Ω, ZC = 100 Ω và R = 100 Ω
Và ta tính được tổng trở của mạch \ ( Z = 100 \ sqrt 2 \ Omega \ )
Điện áp hiệu dụng hai đầu đoạn mạch khi đó là U = IZ = 100 V
+ Khi vận tốc quay của động cơ là n0 thì điện áp hiệu dụng hai đầu tụ điện đạt giá trị cực lớn, tần số của dòng điện trong mạch khi đó là f0
Ta có \ ( { f_0 } = \ frac { 1 } { { 2 \ pi \ sqrt { LC } } } = 25 \ sqrt 2 Hz \ )
Khi đó vận tốc quay của động cơ là \ ( { n_0 } = \ frac { { 60 { f_0 } } } { p } = 750 \ sqrt 2 \ ) vòng / phút
Mặt khác, điện áp hiệu dụng hai đầu đoạn mạch khi này là
\ ( \ frac { { { U_0 } } } { U } = \ frac { { { f_0 } } } { f } = \ frac { { 25 \ sqrt 2 } } { { 50 } } = \ frac { { \ sqrt 2 } } { 2 } \ Rightarrow { U_0 } = \ frac { { 100 \ sqrt 2 } } { 2 } = 50 \ sqrt 2 V \ )
Điện áp hiệu dụng hai đầu tụ điện khi này
\ ( { U_C } = \ frac { { { U_0 } } } { R }. { Z_C } = \ frac { { 50 \ sqrt 2 } } { { 100 } }. \ frac { 1 } { { 2 \ pi. 25 \ sqrt 2. \ frac { { { { 10 } ^ { – 4 } } } } { \ pi } } } = 100V \ )
Chọn AĐáp án – Lời giải Câu hỏi 11 :Hai máy phát điện xoay chiều một pha đang hoạt động giải trí thông thường và tạo ra hai suất điện động có cùng tần số f. Rôto của máy thứ nhất có p1 cặp cực quay với vận tốc n1 = 1800 vòng / phút. Rôto của máy thứ hai có p2 = 4 cặp cực quay với vận tốc n2. Biết n2 có giá trị trong khoảng chừng từ 12 vòng / giây đến 18 vòng / giây. Giá trị của f là ?

• A48Hz 
• B54Hz 
• C60Hz 
• D50Hz 

Đáp án: C

Phương pháp giải :sử dụng công thức tính tân số của dòng điệnLời giải cụ thể :Ta có :

\(\begin{gathered}
f = {p_1}.{n_1} = {p_2}.{n_2} \hfill \\
\Leftrightarrow {p_1}.30 = 4.{n_2} \hfill \\
\end{gathered} \)

Tần số f là ước chung của 30 và 4 là 60, 120 …. Vì biết rằng n2 nằm trong khoảng chừng 12 đến 18 vòng / s. nên f = 60 Hz .Đáp án – Lời giải Câu hỏi 12 :

Một máy phát điện xoay chiều một pha, rô to có hai cặp cực. Nối hai cực của máy phát với đoạn mạch AB gồm R, cuộn cảm thuần và tụ điện nối tiếp nhau. Cho R = 69,1 Ω điện dung \(C = {{{{10}^{ – 4}}} \over {0,18\pi }}F\). Khi rô to của máy phát quay đều với tốc độ 1200 vòng/phút hoặc 2268 vòng/phút thì công suất tiêu thụ của đoạn mạch AB là như nhau. Độ tự cảm của cuộn dây có giá trị gần nhất với giá trị

• A0,6 H.
• B0,8 H.     
• C 0,2 H.
• D0,4 H.

Đáp án: A

Lời giải chi tiết cụ thể :

Đáp án A

+ Công suất tiêu thụ của mạch : \ ( P = { { { U ^ 2 } R } \ over { { R ^ 2 } + { { \ left ( { L \ omega – { 1 \ over { C \ omega } } } \ right ) } ^ 2 } } } \ ) với \ ( U = k \ omega \ ), k là thông số tỉ lệ .
Biến đổi toán học, ta thu được : \ ( { 1 \ over { { C ^ 2 } } } { 1 \ over \ omega } – \ left ( { { { 2L } \ over C } – { R ^ 2 } } \ right ) { 1 \ over { { \ omega ^ 2 } } } + \ left ( { { L ^ 2 } – { { { k ^ 2 } R } \ over P } } \ right ) = 0. \ )
Hai giá trị của tần số góc cho cùng hiệu suất tiêu thụ trên mạch thỏa mãn nhu cầu : \ ( { 1 \ over { \ omega _1 ^ 2 } } + { 1 \ over { \ omega _2 ^ 2 } } = 2LC – { R ^ 2 } { C ^ 2 }. \ )
+ Với \ ( \ omega = 2 \ pi n \ ) thay những giá trị vào phương trình trên ta tìm được \ ( L \ approx 0,63 H. \ )Đáp án – Lời giải Câu hỏi 13 :Tại một điểm M có một máy phát điện xoay chiều một pha có hiệu suất phát điện và điện áp hiệu dụng ở hai cực của máy phát đều không đổi. Điện năng được truyền đến nơi tiêu thụ trên một đường dây có điện trở không đổi. Coi thông số hiệu suất của mạch luôn bằng 1. Hiệu suất của quy trình truyền tải này là H. Muốn tăng hiệu suất quy trình truyền tải lên đến 97,5 % nên trước khi truyền tải, nối hai cực của máy phát điện với cuộn sơ cấp của máy biến áp lí tưởng và cuộn thứ cấp được nối với dây tải. Nhưng trong quy trình nối, do bị nhầm giữa cuộn sơ cấp và thứ cấp nên hiệu suất quy trình truyền tải chỉ là 60 %. Giá trị của H và tỉ số số vòng dây ở cuộn sơ cấp và thứ cấp ( k = N1 / N2 ) của máy biến áp là

• A H = 78,75%; k = 0,25
• BH = 90%; k = 0,5. 
• CH = 78,75%; k = 0,5
• DH = 90%; k = 0,25. 

Đáp án: B

Phương pháp giải :Sử dụng công thức hiệu suất truyền tải và tính hiệu suất hao phíLời giải cụ thể :Gọi hiệu suất truyền tải là P, hiệu điện thế phát là U, ta có :

\(\begin{array}{l}
{P_{hp}} = {I^2}.R = \frac{{{P^2}}}{{{U^2}}}.R;H = \frac{{P – {P_{hp}}}}{P} \Rightarrow {P_{hp}} = P – H.P = (1 – H).P \Rightarrow 1 – H \sim \frac{1}{{{U^2}}}\\
\Rightarrow \left\{ \begin{array}{l}
1 – 97,5\% \sim \frac{1}{{{{(\frac{1}{k}U)}^2}}}\\
1 – 60\% \sim \frac{1}{{{{(k.U)}^2}}}
\end{array} \right. \Rightarrow \frac{{1 – 97,5\% }}{{1 – 60\% }} = {k^4} \Leftrightarrow {k^4} = \frac{1}{{16}} \Rightarrow k = 0,5 \Rightarrow \frac{{1 – H}}{{1 – 60\% }} = {k^2} = \frac{1}{4} \Rightarrow H = 90\%
\end{array}\)

Đáp án – Lời giải Câu hỏi 14 :Nối hai cực của một máy phát điện xoay chiều một pha vào hai đầu đoạn mạch AB gồm điện trở thuần R mắc tiếp nối đuôi nhau với cuộn cảm thuần. Bỏ qua điện trở những cuộn dây của máy phát. Khi roto của máy quay đều với vận tốc n vòng / phút thì cường độ dòng điện hiệu dụng trong đoạn mạch là 1A. Khi roto của máy quay đều với vận tốc 3 n vòng / phút thì cường độ dòng điện hiệu dụng trong đoạn mạch là \ ( \ sqrt 3 \ ) A. Nếu roto của máy quay đều với vận tốc 2 n vòng / phút thì cảm kháng của đoạn mạch AB là

• A\(\frac{R}{{\sqrt 3 }}\)      
• B\(R\sqrt 3 \)      
• C\(\frac{{2R}}{{\sqrt 3 }}\)    
• D\(2R\sqrt 3 \)

Đáp án: C

Phương pháp giải :Vận dụng biểu thức tính hiệu điện thế : U = IZLời giải chi tiết cụ thể :

Đáp áp C

Khi roto của máy quay đều với vận tốc n vòng / phút
\ ( U = 1 \ sqrt { { R ^ 2 } + { Z_L } ^ 2 } \ ) ( 1 )
Khi roto của máy quay đều với vận tốc 3 n vòng / phút
\ ( 3U = \ sqrt 3 \ sqrt { { R ^ 2 } + 9 { Z_L } ^ 2 } \ ) ( 2 )
Từ ( 1 ) và ( 2 ) \ ( \ to \ frac { { \ sqrt 3 \ sqrt { { R ^ 2 } + 9 { Z_L } ^ 2 } } } { { \ sqrt { { R ^ 2 } + { Z_L } ^ 2 } } } = \ frac { { 3U } } { U } \ to { Z_L } = \ frac { R } { { \ sqrt 3 } } \ )
Nếu roto của máy quay đều với vận tốc 2 n vòng / phút thì :
\ ( { Z_ { { L_0 } } } = 2 { Z_L } = \ frac { { 2R } } { { \ sqrt 3 } } \ )Đáp án – Lời giải Câu hỏi 15 :Một động cơ không đồng bộ ba pha được mắc theo hình tam giác. Ba đỉnh của tam giác này được mắc vào ba dây pha của một mạng điện ba pha hình sao với điện áp pha hiệu dụng \ ( \ frac { { 220 } } { { \ sqrt 3 } } V \ ). Động cơ đạt hiệu suất 3 kW và có thông số hiệu suất \ ( \ cos \ varphi = \ frac { { 10 } } { { 11 } } \ ). Tính cường độ dòng điện hiệu dụng qua mỗi cuộn dây của động cơ .

• A\(10A\)   
• B\(2,5A\)   
• C\(2,5\sqrt 2 A\)   
• D5A

Đáp án: C

Phương pháp giải :Vận dụng biểu thức khi 3 pha mắc hình tam giác : \ ( { U_d } = \ sqrt 3 { U_p }, { I_d } = { I_p } \ )Lời giải chi tiết cụ thể :

Đáp án D

Ba đỉnh của tam giác này được mắc vào ba dây pha của một mạng điện ba pha hình sao
\ ( { U_d } = \ sqrt 3 { U_p } = 220 ( V ) \ )
Ta có : \ ( P = { U_d } { I_d } { \ rm { cos } } \ varphi \ to { { \ rm { I } } _d } = \ frac { P } { { { U_d } { \ rm { cos } } \ varphi } } = 15 ( A ) \ )
Do đó cường độ hiệu dụng qua mỗi cuộn dây là \ ( I = \ frac { { { I_d } } } { 3 } = 5 { \ rm { } } A \ )Đáp án – Lời giải Câu hỏi 16 :Một động cơ điện xoay chiều sản ra hiệu suất cơ học 7,5 kW và có hiệu suất 80 %. Mắc động cơ tiếp nối đuôi nhau với một cuộn cảm rồi mắc chúng vào mạng điện xoay chiều. Giá trị hiệu điện thế hiệu dụng ở hai đầu động cơ là UM biết rằng dòng điện qua động cơ có cường độ hiệu dụng I = 40A và trễ pha với uM một góc \ ( \ pi / 6 \ ). Hiệu điện thế ở hai đầu cuộn cảm UL = 125V và sớm pha so với dòng điện qua cuộn cảm là \ ( \ pi / 3 \ ). Tính điện áp hiệu dụng của mạng điện và độ lệch pha của nó so với dòng điện .

• A384V; 400 
• B 834V; 450
• C384V; 390         
• D184V; 390

Đáp án: C

Phương pháp giải :

+ Vận dụng biểu thức tính công suất

+ Áp dụng định lý hàm số cos trong tam giácLời giải chi tiết cụ thể :

Đáp án C

Ta có
\ ( \ begin { array } { l } P { \ rm { } } = { \ rm { } } { P_ { cohoc } }. \ frac { { 100 } } { { 80 } } = 9,375 { \ rm { } } KW \ \ \ to { U_M } = { \ rm { } } \ frac { P } { { Ic { \ rm { os } } \ frac { \ pi } { 6 } } } = 270,633 { \ rm { } } V \ end { array } \ )

Áp dụng định lý cos trong tam giác ta có :

 

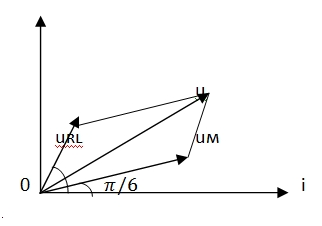
\(\eqalign{
& U = {\rm{ }}U{_{RL}}{\rm{ }} + {\rm{ }}U{_M}{\rm{ }} – {\rm{ }}2{U_{RL}}.{U_L}.cos{150^0} \cr
& \to {\rm{ }}U = 384{\rm{ }}V \cr} \)

gọi \ ( \ left ( { u ; { \ rm { } } { u_M } } \ right ) = \ varphi \ to U { _ { RL } } { \ rm { } } = U { \ rm { } } + U { _M } – 2. U. { U_M }. cos \ varphi \ to \ varphi = { 9 ^ 0 } \ )
=> góc hợp bởi u và i là 390Đáp án – Lời giải Câu hỏi 17 :Một máy phát điện xoay chiều một pha có điện trở không đáng kể, được mắc với mạch ngoài là một đoạn mạch mắc tiếp nối đuôi nhau gồm điện trở thuần R, tụ điện C và cuộn cảm thuần L. Khi vận tốc quay của roto là n1 và n2 thì cường độ dòng điện hiệu dụng trong mạch có cùng giá trị. Khi vận tốc quay là n0 thì cường độ dòng điện hiệu dụng trong mạch đạt cực lớn. Mối liên hệ giữa n1, n2 và n0 là

• A\(n_0^2 = {n_1}.{n_2}\)
• B\(n_0^2 = \frac{{2n_1^2.n_2^2}}{{n_1^2 + n_2^2}}\)   
• C\(n_o^2 = \frac{{n_1^2 + n_2^2}}{2}\) 
• D\(n_0^2 = n_1^2 + n_2^2\)

Đáp án: B

Phương pháp giải :

+ Vận dụng biểu thức tính cường độ dòng điện

+ Khảo sát hàm số bậc 2Lời giải chi tiết cụ thể :

 Đáp án B

Ta có :
\ ( I = \ frac { { { E_0 } } } { Z } = \ frac { { \ omega { \ Phi _0 } } } { { \ sqrt { { R ^ 2 } + { { ( { Z_L } – { Z_C } ) } ^ 2 } } } } = \ frac { { { \ Phi _0 } } } { { \ sqrt { \ frac { 1 } { { { C ^ 2 } { \ omega ^ 4 } } } – \ frac { { \ frac { { 2L } } { C } – { R ^ 2 } } } { { { \ omega ^ 2 } } } + { L ^ 2 } } } } = \ frac { { { \ Phi _0 } } } { { \ sqrt y } } \ )
IMaxkhi ymin
\ ( \ to \ frac { 1 } { { { \ omega _0 } ^ 2 } } = \ frac { { \ frac { { 2L } } { C } – { R ^ 2 } } } { { \ frac { 2 } { { { C ^ 2 } } } } } = LC – \ frac { { { R ^ 2 } { C ^ 2 } } } { 2 } \ )
\ ( \ begin { array } { l } { I_1 } = { I_2 } \ to { y_1 } = { y_2 } \ \ \ to \ frac { 1 } { { \ omega _1 ^ 2 } } + \ frac { 1 } { { \ omega _2 ^ 2 } } = \ frac { 2 } { { \ omega _0 ^ 2 } } \ to \ omega _0 ^ 2 = \ frac { { 2 { \ omega _1 } { \ omega _2 } } } { { \ omega _1 ^ 2 + \ omega _2 ^ 2 } } \ end { array } \ )
Vì \ ( \ omega \ ) tỉ lệ thuận với n, ta suy ra :
\ ( \ to n_0 ^ 2 = \ frac { { 2 { n_1 } { n_2 } } } { { n_1 ^ 2 + n_2 ^ 2 } } \ )Đáp án – Lời giải Câu hỏi 18 :Một máy phát điện xoay chiều một pha có phần ứng gồm bốn cuộn dây mắc tiếp nối đuôi nhau. Suất điện động xoay chiều do máy phát sinh ra có tần số 50H z và giá trị hiệu dụng 200 \ ( \ sqrt { 2 } \ ) V. Từ thông cực lớn qua mỗi vòng của phần ứng là \ ( \ frac { 5 } { \ pi } \ ) mWb. Số vòng dây trong mỗi cuộn dây của phần ứng là :

• A200 vòng            
• B400 vòng
• C141 vòng
• D282 vòng

Đáp án: A

Phương pháp giải :Công thức tính suất điện động xoay chiều : E0 = ωNBS = ω \ ( { { \ phi } _ { 0 } } \ )
Liên hệ giữa tần số và vận tốc góc ω = 2 πf
Liên hệ giữa giá trị cực lớn và giá trị hiệu dụng : \ ( { { E } _ { 0 } } = E \ sqrt { 2 } \ )Lời giải cụ thể :Ta có : E0 = ωNBS = ωN \ ( { { \ phi } _ { 0 } } \ ) = 400V
— > 2 π. 50. N. \ ( \ frac { 5 } { \ pi } { {. 10 } ^ { – 3 } } \ ) = 400V — > N = 800 vòng
Vậy mỗi cuộn dây có 800 : 4 = 200 vòng dâyĐáp án – Lời giải Câu hỏi 19 :Nối hai cực của một máy phát điện xoay chiều một pha vào hai đầu mạch AB gồm điện trở thuần R mắc tiếp nối đuôi nhau với cuộn cảm thuần. Bỏ qua điện trở những cuộn dây của máy phát. Khi rô to của máy quay đều với vận tốc n vòng / phút thì cường độ dòng điện hiệu dụng trong mạch là 1A. Khi rô to của máy quay đều với vận tốc 3 n vòng / phút thì cường độ dòng điện hiệu dụng trong mạch là \ ( \ sqrt { 3 } \ ) A. Nếu rô to của máy quay đều với vận tốc 2 n vòng / phút thì cảm kháng của đoạn mạch AB là

• A\(2R\sqrt{3}\)
• B\(\frac{2R}{\sqrt{3}}\)
• C\(\frac{R}{\sqrt{3}}\)
• D\(R\sqrt{3}\)

Đáp án: C

Phương pháp giải :Định luật Ôm : I = U / Z
Tốc độ quay của roto tỉ lệ với hiệu điện thế thu đượcLời giải cụ thể :Ta có : \ ( \ frac { { { I } _ { 1 } } } { { { I } _ { 2 } } } = \ frac { { { U } _ { 1 } } } { { { U } _ { 2 } } }. \ frac { { { Z } _ { 2 } } } { { { Z } _ { 1 } } } \ Rightarrow \ frac { 1 } { \ sqrt { 3 } } = \ frac { 1 } { 3 } \ sqrt { \ frac { { { R } ^ { 2 } } + 9Z _ { L } ^ { 2 } } { { { R } ^ { 2 } } + Z_ { L } ^ { 2 } } } \ Rightarrow { { Z } _ { L } } = \ frac { R } { \ sqrt { 3 } } \ )

 Chọn C

Đáp án – Lời giải Câu hỏi 20 :Nối hai cực của một máy phát điện xoay chiều một pha vào hai đầu đoạn mạch AB mắc tiếp nối đuôi nhau gồm điện trở R = 52 Ω, cuộn cảm thuần có độ tự cảm L = 0,6 H và tụ điện có điện dung 126 µF và một ampe kế lí tưởng. Bỏ qua điện trở thuần của những cuộn dây của máy phát. Biết roto của máy phát có hai cặp cực. Để số chỉ của ampe kế đạt giá trị cực lớn, rô to của máy phát phải quay với vận tốc gần nhất với tác dụng nào sau đây ?

• A328 vòng/phút
• B650 vòng/phút
• C465 vòng/phút
• D528 vòng/phút

Đáp án: B

Phương pháp giải :Tần số \ ( f = \ frac { \ omega } { 2 \ pi } \ )
Tần số do máy phát điện xoay chiều có p cặp cực tạo ra là f = np
Suất điện động do máy phát xoay chiều tạo ra có E = ωφ
Định luật Ôm cho đoạn mạch : I = E / Z
Tổng trở \ ( Z = \ sqrt { { { R } ^ { 2 } } + { { ( { { Z } _ { L } } – { { Z } _ { C } } ) } ^ { 2 } } } \ )Lời giải chi tiết cụ thể :Dòng điện trong mạch :
\ ( I = \ frac { E } { Z } = \ frac { \ omega \ phi } { \ sqrt { { { R } ^ { 2 } } + { { ( { { Z } _ { L } } – { { Z } _ { C } } ) } ^ { 2 } } } } = \ frac { \ phi } { \ sqrt { \ frac { { { R } ^ { 2 } } } { { { \ omega } ^ { 2 } } } – { { L } ^ { 2 } } – \ frac { 2L } { C { { \ omega } ^ { 2 } } } + \ frac { 1 } { { { \ omega } ^ { 4 } } { { C } ^ { 2 } } } } } \ )
Đặt y = \ ( \ frac { { { R } ^ { 2 } } } { { { \ omega } ^ { 2 } } } – { { L } ^ { 2 } } – \ frac { 2L } { C { { \ omega } ^ { 2 } } } + \ frac { 1 } { { { \ omega } ^ { 4 } } { { C } ^ { 2 } } } \ )
Để Imax thì y min hay y ’ = 0
Khi đó : \ ( – \ frac { 2 { { R } ^ { 2 } } } { { { \ omega } ^ { 3 } } } + \ frac { 4L } { C { { \ omega } ^ { 3 } } } – \ frac { 4 } { { { C } ^ { 2 } } { { \ omega } ^ { 5 } } } = 0 \ Rightarrow { { \ omega } ^ { 2 } } \ left ( \ frac { 4L } { C } – 2 { { R } ^ { 2 } } \ right ) = \ frac { 4 } { { { C } ^ { 2 } } } \ Rightarrow \ omega = 135,9 rad / s \ to f = 21,63 Hz \ )
Mà f = np = 2 n — > n = 10,815 vòng / s = 649 vòng / phút

Chọn B

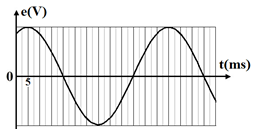
Đáp án – Lời giải Câu hỏi 21 :Máy phát điện xoay chiều một pha nam châm từ có p cặp cực quay với vận tốc 100 ( vòng / phút ) tạo ra suất điện động có đồ thị nhờ vào thời hạn như hình vẽ. Số cặp cực p của máy phát điện là

• A12                    
• B5                 
• C10               
• D 15

Đáp án: C

Phương pháp giải :Áp dụng công thức tần số : f = p. n
Với p là số cặp cực, n là vận tốc quay của roto ( vòng / giây )Lời giải chi tiết cụ thể :Từ hình vẽ ta xác lập được chu kì : T = 12.5 = 60 ms .
Ta có :
\ ( f = \ frac { 1 } { T } = \ frac { 1 } { { 60 } } {. 10 ^ 3 } = \ frac { { 100 } } { 6 } Hz \ )
Lại có : f = p. n với p là số cặp cực, n là vận tốc quay của roto ( vòng / giây ) .
Vậy số cặp cực là :
\ ( p = \ frac { f } { n } = \ frac { { 100 } } { 6 } : \ frac { { 100 } } { { 60 } } = 10 \ )

Chọn C

Đáp án – Lời giải Câu hỏi 22 :Một máy phát điện lý tưởng gồm hai cuộn dây N1 và N2, được cấp bởi nguồn điện xoay chiều có biên độ và tần số không đổi. Nếu nối hai đầu cuộn N1 vào nguồn điện và cuộn N2 vào điện trở R thì hiệu suất tiêu thụ trên R là 100W. Nếu nối hai đầu cuộn N2 vào nguồn điện và hai đầu cuộn N1 với điện trở R thì hiệu suất tiêu thụ trên R là 400W. Nếu đặt nguồn điện vào hai đầu điện trở R thì hiệu suất tiêu thụ trên R là

• A250W 
• B200W
• C225W
• D300W

Đáp án: B

Phương pháp giải :Áp dụng công thức \ ( \ frac { { { U_1 } } } { { { U_2 } } } = \ frac { { { N_1 } } } { { { N_2 } } } \ )
Công thức tính hiệu suất \ ( P = { I ^ 2 }. R = \ frac { { { U ^ 2 } } } { R } \ )Lời giải cụ thể :

Cách giải:

Ta có :

\(\begin{array}{l}\left\{ {\begin{array}{*{20}{l}}{{P_1} = {I_1}^2.R = \frac{{{U_1}^2}}{R} = 100W}\\{{P_2} = {I_2}^2.R = \frac{{{U_2}^2}}{R} = 400W}\end{array}} \right.\\\frac{{{U_2}}}{{{U_1}}} = \frac{{U.\frac{{{N_1}}}{{{N_2}}}}}{{U\frac{{{N_2}}}{{{N_1}}}}} = {\left( {\frac{{{N_1}}}{{{N_2}}}} \right)^2} \Rightarrow \frac{{{P_2}}}{{{P_1}}} = {\left( {\frac{{{U_2}}}{{{U_1}}}} \right)^2} = {\left( {\frac{{{N_1}}}{{{N_2}}}} \right)^4} = 4\\ \Rightarrow \frac{{{N_1}}}{{{N_2}}} = \sqrt 2  \Rightarrow {U_2} = \sqrt 2 .U \Rightarrow P = \frac{{{U^2}}}{R} = \frac{{U_2^2}}{{2.R}} = \frac{{400}}{2} = 200{\rm{W}}\end{array}\)

Chọn B

Đáp án – Lời giải Câu hỏi 23 :Nếu vận tốc quay của roto tăng thêm l vòng / s thì tần số của dòng điện do máy phát điện xoay chiều 1 pha phát ra tăng từ 60 Hz đến 70 Hz và suất điện động hiệu dụng do máy phát ra biến hóa 40 V so với khởi đầu. Hỏi nếu liên tục tăng vận tốc của roto thêm 2 vòng / s nữa thì suất điện động hiệu dụng do máy phát ra là bao nhiêu ?

• A360 V. 
• B400 V.
• C320V.
• D280 V .

Đáp án: A

Phương pháp giải :Tần số của dòng điện và suất điện động do máy phát điện xoay chiều 1 pha phát ra tỉ lệ thuận với vận tốc quay của rotoLời giải cụ thể :Tần số của dòng điện do máy phát ra tỉ lệ thuận với vận tốc quay của roto
\ ( \ to \ frac { { { n } _ { 1 } } } { { { n } _ { 2 } } } = \ frac { { { f } _ { 1 } } } { { { f } _ { 2 } } } \ to \ frac { { { n } _ { 1 } } } { { { n } _ { 1 } } + 1 } = \ frac { 6 } { 7 } \ to { { n } _ { 1 } } = 6 \ )
Suất điện động do máy phát ra tỉ lệ thuận với vận tốc quay của roto
\ ( \ to \ frac { { { E } _ { 1 } } } { { { E } _ { 2 } } } = \ frac { { { n } _ { 1 } } } { { { n } _ { 2 } } } \ to \ frac { { { E } _ { 1 } } } { { { E } _ { 1 } } + 40 } = \ frac { 6 } { 7 } \ to { { E } _ { 1 } } = 240 ( V ) \ )
\ ( \ frac { { { E } _ { 1 } } } { { { E } _ { 3 } } } = \ frac { { { n } _ { 1 } } } { { { n } _ { 3 } } } \ to \ frac { { { E } _ { 1 } } } { { { E } _ { 3 } } } = \ frac { 6 } { 9 } \ to { { E } _ { 3 } } = 360 ( V ) \ )

Chọn A

Đáp án – Lời giải Câu hỏi 24 :Một máy phát điện xoay chiều có roto nam châm hút gồm 8 cực Nam, Bắc xen kẽ. Tốc độ quay của roto là 750 ( vòng / phút ). Phần ứng gồm 4 cuộn dây giống nhau mắc tiếp nối đuôi nhau. Tính số vòng của mỗi cuộn dây biết từ thông cực lớn qua mỗi vòng dây là \ ( { \ Phi _0 } = 0,005 Wb \ ) và suất điện động hiệu dụng mà máy tạo ra là 220V :

• A200         
• B140    
• C50       
• D35

Đáp án: C

Phương pháp giải :+ Công thức tính tần số của suất điện động do máy phát điện sinh ra : \ ( f = \ dfrac { { n. p } } { { 60 } } \ )
Trong đó : n ( vòng / phút ) là vận tốc quay của roto ; p là số cặp cực
+ Công thức tính suất điện động hiệu dụng : \ ( E = \ dfrac { { \ omega. N. { \ Phi _0 } } } { { \ sqrt 2 } } \ )Lời giải cụ thể :Tần số của suất điện động do máy phát điện sinh ra là :
\ ( f = \ dfrac { { n. p } } { { 60 } } = \ dfrac { { 750.4 } } { { 60 } } = 50H z \ Rightarrow \ omega = 100 rad / s \ )
Suất điện động hiệu dụng mà máy tạo ra :
\ ( E = \ dfrac { { \ omega. N. { \ Phi _0 } } } { { \ sqrt 2 } } \ Rightarrow N = \ dfrac { { E \ sqrt 2 } } { { \ omega. { \ Phi _0 } } } = \ dfrac { { 220 \ sqrt 2 } } { { 100 \ pi. 0,005 } } = 198 \ )
Số vòng dây mỗi cuộn là : \ ( { N_1 } = \ dfrac { N } { 4 } = \ dfrac { { 198 } } { 4 } \ approx 50 \ )

Chọn C.

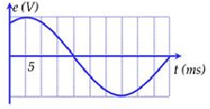
Đáp án – Lời giải Câu hỏi 25 :Máy phát điện xoay chiều một pha có p cặp cực ( p cực nam, p cực bắc ) quay với vận tốc \ ( 1000 \ ) ( vòng / phút ) tạo ra suất điện động có đồ thị nhờ vào thời hạn như hình vẽ. Giá trị của p là

• A10
• B2
• C1
• D5

Đáp án: C

Phương pháp giải :- Đọc đồ thị
– Vận dụng biểu thức : \ ( T = \ dfrac { 1 } { f } \ )
– Vận dụng biểu thức tần số của máy phát điện xoay chiều : \ ( f = np \ )Lời giải cụ thể :Từ đồ thị, ta có chu kì giao động \ ( T = 12 \ ) ô \ ( = { 12.5.10 ^ { – 3 } } = 0,06 s \ )
\ ( \ Rightarrow f = \ dfrac { 1 } { T } = \ dfrac { { 50 } } { 3 } \ left ( { Hz } \ right ) \ )
Ta có, vận tốc quay của máy phát : \ ( n = 1000 \ ) vòng / phút \ ( = \ dfrac { { 50 } } { 3 } \ ) vòng / s
Lại có : \ ( f = np \ Rightarrow p = \ dfrac { f } { n } = \ dfrac { { \ dfrac { { 50 } } { 3 } } } { { \ dfrac { { 50 } } { 3 } } } = 1 \ )

Chọn C

Đáp án – Lời giải Câu hỏi 26 :Một máy phát điện xoay chiều một pha có điện trở trong không đáng kể. Nối hai cực của máy phát với một đoạn mạch gồm một điện trở mắc tiếp nối đuôi nhau với một cuộn cảm thuần. Khi rôto của máy phát quay đều với vận tốc góc n vòng / s thì cường độ dòng điện hiệu dụng trong mạch là \ ( 2 \ sqrt 3 \, \, A \ ) và thông số hiệu suất của mạch bằng \ ( \ dfrac { { \ sqrt 3 } } { 2 } \ ). Nếu rôto quay đều với vận tốc góc là 3 n vòng / s thì cường độ dòng điện hiệu dụng trong mạch là

• A4 A     
• B 6 A   
• C \(4\sqrt 3 \,\,A\) 
• D\(4\sqrt 2 \,\,A\)

Đáp án: B

Phương pháp giải :Cảm kháng của cuộn dây : \ ( { Z_L } = \ omega L \ )
Hệ số hiệu suất của đoạn mạch xoay chiều : \ ( \ cos \ varphi = \ dfrac { R } { { \ sqrt { { R ^ 2 } + { Z_L } ^ 2 } } } \ )
Suất điện động hiệu dụng của máy phát điện : \ ( E = \ dfrac { { NBS \ omega } } { { \ sqrt 2 } } \ )
Cường độ dòng điện hiệu dụng : \ ( I = \ dfrac { E } { { \ sqrt { { R ^ 2 } + { Z_L } ^ 2 } } } \ )Lời giải chi tiết cụ thể :Khi rôto quay với vận tốc ꞷ = n vòng / s, thông số hiệu suất của mạch là :
\ ( \ begin { array } { l } \ cos \ varphi = \ dfrac { R } { { \ sqrt { { R ^ 2 } + { Z_L } ^ 2 } } } = \ dfrac { { \ sqrt 3 } } { 2 } \ \ \ Rightarrow 4 { R ^ 2 } = 3 { R ^ 2 } + 3 { Z_L } ^ 2 \ Rightarrow { R ^ 2 } = 3 { Z_L } ^ 2 \ Rightarrow { Z_L } = \ dfrac { R } { { \ sqrt 3 } } \ end { array } \ )
Cường độ dòng điện hiệu dụng trong mạch là :
\ ( I = \ dfrac { E } { { \ sqrt { { R ^ 2 } + { Z_L } ^ 2 } } } = 2 \ sqrt 3 \ Rightarrow \ dfrac { E } { { \ sqrt { { R ^ 2 } + \ dfrac { { { R ^ 2 } } } { 3 } } } } = 2 \ sqrt 3 \ Rightarrow E = 4R \ )
Khi quay với vận tốc ꞷ ’ = 3 n vòng / s, cảm kháng của cuộn dây và suất điện động hiệu dụng của máy phát là :
\ ( \ left \ { \ begin { array } { l } { Z_L } ‘ = 3 { Z_L } \ Rightarrow { Z_L } ‘ = R \ sqrt 3 \ \ E ‘ = 3E = 12R \ end { array } \ right. \ )
Cường độ dòng điện hiệu dụng trong mạch khi đó là :
\ ( I ‘ = \ dfrac { U } { { \ sqrt { { R ^ 2 } + { Z_L } { ‘ ^ 2 } } } } = \ dfrac { { 12R } } { { \ sqrt { { R ^ 2 } + { { \ left ( { \ sqrt 3 R } \ right ) } ^ 2 } } } } = 6 \, \, \ left ( A \ right ) \ )

Chọn B.

Đáp án – Lời giải Câu hỏi 27 :Một máy phát diện xoay chiều một pha phát ra dòng điện có tần số 60 Hz để duy trì hoạt động giải trí của một thiết bị kĩ thuật ( chỉ hoạt động giải trí với dòng điện có tần số 60 Hz ). Nếu thay roto của nó bằng một roto khác có nhiều hơn một cặp cực thì số vòng xoay của roto trong một giờ biến hóa 7200 vòng. Tính số cặp cực của roto bắt đầu

• A4
• B5
• C10
• D15

Đáp án: B

Phương pháp giải :Tần số của máy phát điện xoay chiều : \ ( f = np \ ) với p là số cặp cực, n là số vòng xoay của roto trong 1 giâyLời giải cụ thể :Tần số của máy phát điện khi chưa đổi khác số cặp cực là : \ ( f = np = 60 \, \, \ left ( { Hz } \ right ) \ )
Khi thay roto của máy phát điện bằng một roto khác có nhiều hơn 1 cặp cực, số vòng xoay của roto đổi khác trong 1 giây là : \ ( n ‘ = n – \ dfrac { { 7200 } } { { 3600 } } = n – 2 \ ) ( vòng / s )
Tần số của máy phát điện không đổi nên :
\ ( \ begin { array } { l } \ left ( { n – 2 } \ right ). \ left ( { p + 1 } \ right ) = np = 60 \, \, \ left ( { Hz } \ right ) \ \ \ Rightarrow n – 2 p – 2 = 0 \ Rightarrow n = 2 p + 2 \ \ \ Rightarrow p. \ left ( { 2 p + 2 } \ right ) = 60 \ Rightarrow 2 { p ^ 2 } + 2 p – 60 = 0 \ \ \ Rightarrow \ left [ \ begin { array } { l } p = 5 \, \, \, \ left ( { t / m } \ right ) \ \ p = – 6 \, \, \ left ( { loai } \ right ) \ end { array } \ right. \ end { array } \ )
Vậy số cặp cực khởi đầu của roto là 5 cặp

Chọn B.

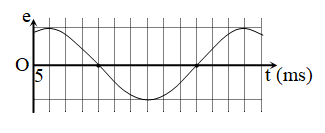
Đáp án – Lời giải Câu hỏi 28 :Máy phát điện xoay chiều một pha có p cặp cực ( p cực nam, p cực bắc ) quay với vận tốc \ ( 1000 \, \, \ left ( { vong / phut } \ right ) \ ) tạo ra suất điện động có đồ thị nhờ vào thời hạn như hình vẽ. Giá trị của p là

• A\(5\). 
• B\(1\). 
• C\(2\).      
• D\(10\).

Đáp án: B

Phương pháp giải :Sử dụng kĩ năng đọc đồ thị
Tần số của suất điện động : \ ( f = \ dfrac { { np } } { { 60 } } \ )Lời giải chi tiết cụ thể :Độ chia nhỏ nhất của 1 ô theo phương ngang là \ ( 5 \, \, \ left ( { ms } \ right ) \ )

Nhận xét : khoảng cách giữa 2 điểm A và B trên đồ thị là 1 nửa chu kì tương tự với 6 ô
\ ( \ Rightarrow \ dfrac { T } { 2 } = 6.5 = 30 \, \, \ left ( { ms } \ right ) \ Rightarrow T = 60 \, \, \ left ( { ms } \ right ) \ )
Tần số của suất điện động là : \ ( f = \ dfrac { 1 } { T } = \ dfrac { 1 } { { { { 60.10 } ^ { – 3 } } } } = \ dfrac { { 50 } } { 3 } \, \, \ left ( { Hz } \ right ) \ )
Ta có : \ ( f = \ dfrac { { np } } { { 60 } } \ Rightarrow p = \ dfrac { { 60 f } } { n } = \ dfrac { { 60. \ dfrac { { 50 } } { 3 } } } { { 1000 } } = 1 \ )

Chọn B.

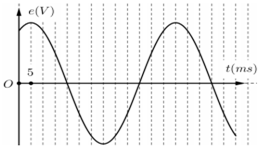
Đáp án – Lời giải Câu hỏi 29 :Máy phát điện xoay chiều một pha, nam châm hút có 10 cặp cực quay với vận tốc \ ( n \ ) ( vòng / phút ) tạo ra suất điện động có đồ thị nhờ vào thời hạn như hình vẽ. Giá trị của \ ( n \ ) là

• A\(200\)
• B\(100\)
• C\(150\)
• D\(50\)

Đáp án: B

Phương pháp giải :Công thức tính tần số của dòng điện xoay chiều sinh ra bởi máy phát điện : \ ( f = \ dfrac { { n. p } } { { 60 } } \ )
Trong đó : \ ( p \ ) là số cặp cực ; \ ( n \ ) ( vòng / phút ) là vận tốc quay của roto .Lời giải cụ thể :Từ đồ thị ta thấy 1 ô ứng với 5 ms .
Một nửa chu kì ứng với 6 ô, một chu kì ứng với 12 ô. Ta có :
\ ( T = 12.5 = 60 ms = 0,06 s \ Rightarrow f = \ dfrac { 1 } { T } = \ dfrac { { 50 } } { 3 } Hz \ )
Mà : \ ( f = \ dfrac { { n. p } } { { 60 } } \ Rightarrow n = \ dfrac { { 60 f } } { p } = \ dfrac { { 60. \ dfrac { { 50 } } { 3 } } } { { 10 } } = 100 \, \ left ( { vong / s } \ right ) \ )

Chọn B.

Đáp án – Lời giải Câu hỏi 30 :

Hai máy phát điện xoay chiều một pha đang hoạt động bình thường và tạo ra hai suất điện động có cùng tần số f. Rôto của máy thứ nhất có p1 cặp cực và quay với tốc độ n1 = 1800 vòng/phút. Rôto của máy thứ hai có p2 = 4 cặp cực và quay với tốc độ n2. Biết n2 có giá trị trong khoảng từ 12 vòng/giây đến 18 vòng/giây. Giá trị của f là

• A54 Hz.                                
• B60 Hz.                               
• C 48 Hz.                                
• D50 Hz.

Đáp án: B

Phương pháp giải :Công thức tính tần số của dòng điện xoay chiều trong máy phát điện \ ( f = p. n \ )

Với p là số cặp cực, n là tốc độ quay của roto có đơn vị là vòng/giây

Lời giải chi tiết cụ thể :Đổi n1 = 1800 vòng / phút = 30 vòng / giây .
Ta có :
\ ( f = { p_1 }. { n_1 } = { p_2 }. { n_2 } \ Rightarrow { p_1 } = \ frac { { { p_2 }. { n_2 } } } { { { n_1 } } } = \ frac { { 4. { n_2 } } } { { 30 } } \ )
Vì n2 từ 12 vòng / giây đến 18 vòng / giây nên :
\ ( \ frac { { 4.12 } } { { 30 } } = 1,6 \ le { p_1 } \ le \ frac { { 4.18 } } { { 30 } } = 2,4 \ Rightarrow { p_1 } = 2 \ Rightarrow { n_2 } = 15 vong / s \ )
Khi đó :
\ ( f = 4.15 = 30.2 = 60 { \ rm { } } Hz \ )

Chọn B.

Đáp án – Lời giải Câu hỏi 31 :Ba suất điện động e1, e2 và e3 được tạo bởi một máy phát điện xoay chiều ba pha. Tại thời gian \ ( { e_1 } = { e_2 } = – 10V \ ) thì suất điện động e3 có giá trị bằng

• A10V  
• B20V       
• C\(20\sqrt 3 V\)   
• D\(10\sqrt 3 V\)

Đáp án: B

Phương pháp giải :Máy phát điện xoay chiều ba pha : \ ( { e_1 } + { e_2 } + { e_3 } = 0 \ )Lời giải chi tiết cụ thể :Ta có : \ ( \ left \ { \ begin { array } { l } { e_1 } + { e_2 } + { e_3 } = 0 \ \ { e_1 } = { e_2 } = – 10V \ end { array } \ right. \ Leftrightarrow \ left ( { – 10 } \ right ) + \ left ( { – 10 } \ right ) + { e_3 } = 0 \ Rightarrow { e_3 } = 20V \ )

Chọn B.

Đáp án – Lời giải Câu hỏi 32 :Nối hai cực của một máy phát điện xoay chiều một pha vào hai đầu đoạn mạch AB gồm điện trở thuần R mắc tiếp nối đuôi nhau với cuộn cảm thuần. Bỏ qua điện trở những cuộn dây của máy phát. Khi rôto của máy quay đều với vận tốc n1 vòng / phút thì cường độ dòng điện hiệu dụng trong đoạn mạch là I ( A ) ; thông số hiệu suất của đoạn mạch AB là \ ( { { \ sqrt 2 } \ over 2 } \ ). Khi rôto của máy quay đều với vận tốc n2 vòng / phút thì cường độ dòng điện hiệu dụng trong đoạn mạch là \ ( { { 2I } \ over { \ sqrt 5 } } \ ). Mối liên hệ của n2 so với n1 là

• A\({n_1} = \sqrt {{2 \over 3}} {n_2}\)
• B\({n_1} = {1 \over 2}{n_2}\)
• C\({n_2} = \sqrt {{2 \over 3}} {n_1}\)
• D\({n_1} = {1 \over 2}{n_1}\)

Đáp án: C

Lời giải cụ thể :

Đáp án C

+ Khi roto quay với vận tốc ta chuẩn hóa \ ( { R_1 } = 1 \ ) và \ ( { Z_ { L1 } } = x \ )
=> Hệ số hiệu suất của mạch \ ( \ cos { \ varphi _1 } = { { { R_1 } } \ over { \ sqrt { R_1 ^ 2 + Z_ { L1 } ^ 2 } } } = { { \ sqrt 2 } \ over 2 } \ leftrightarrow { 1 \ over { \ sqrt { { 1 ^ 2 } + { x ^ 2 } } } } = { { \ sqrt 2 } \ over 2 } \ to x = 1 \ )
+ Khi roto quay với vận tốc \ ( { n_2 } = k { n_1 } \ to { Z_ { L2 } } = kx = k \ )
=> Lập tỉ số \ ( { { { I_2 } } \ over { { I_1 } } } = { { k { Z_1 } } \ over { { Z_2 } } } \ leftrightarrow { 2 \ over { \ sqrt 5 } } = { { k \ sqrt { { 1 ^ 2 } + { 1 ^ 2 } } } \ over { \ sqrt { { 1 ^ 2 } + { k ^ 2 } } } } \ to k = \ sqrt { { 2 \ over 3 } } \ )Đáp án – Lời giải Câu hỏi 33 :Một máy phát điện xoay chiều một pha có điện trở trong không đáng kể. Nối hai cực của máy phát với một đoạn mạch gồm cuộn cảm thuần mắc tiếp nối đuôi nhau với điện trở thuần. Khi roto của may quay đều với vận tốc 3 n vòng / s thì dòng điện trong mạch có cường độ hiệu dụng 3A và thông số hiệu suất của đoạn mạch bằng 0,5. Nếu roto quay đều với vận tốc góc n vòng / s thì cường độ dòng điện hiệu dụng trong mạch bằng

• A3A 
• B\(2\sqrt 2 A\)  
• C2A
• D\(\sqrt 3 A\)

Đáp án: D

Lời giải chi tiết cụ thể :

Đáp án D

Theo bài ra ta có
\ ( \ begin { array } { l } U = E = k. n ; { U_1 } = k. 3 n ; { Z_ { L1 } } = a. 3 n \ \ { I_1 } = \ frac { { k. 3 n } } { { \ sqrt { { R ^ 2 } + { { ( a. 3 n ) } ^ 2 } } } } = 3 ; \, \ cos { \ varphi _1 } = \ frac { R } { { \ sqrt { { R ^ 2 } + { { ( a. 3 n ) } ^ 2 } } } } \ \ 4 { R ^ 2 } = { R ^ 2 } + { ( a. 3 n ) ^ 2 } = > { ( a. 3 n ) ^ 2 } = 3 { R ^ 2 } = > { ( a. n ) ^ 2 } = \ frac { { { R ^ 2 } } } { 3 } \ \ kn = \ sqrt { { R ^ 2 } + 3 { R ^ 2 } } = 2R \ \ { I_2 } = \ frac { { k. n } } { { \ sqrt { { R ^ 2 } + { { ( a. n ) } ^ 2 } } } } = \ frac { { 2R } } { { \ sqrt { { R ^ 2 } + { { \ frac { R } { 3 } } ^ 2 } } } } = \ sqrt 3 \ end { array } \ )Đáp án – Lời giải Câu hỏi 34 :Nối hai cực của một máy phát điện xoay chiều một pha vào hai đầu đoạn mạch AB gồm điện trở thuần R mắc tiếp nối đuôi nhau với cuộn cảm thuần. Bỏ qua điện trở những cuộn dây của máy phát. Khi roto của máy quay đều với vận tốc n vòng / phút thì cường độ dòng điện hiệu dụng trong đoạn mạch là 1A. Khi roto của máy quay đều với vận tốc 3 n vòng / phút thì cường độ dòng điện hiệu dụng trong đoạn mạch là \ ( \ sqrt 3 \ ) A. Nếu roto của máy quay đều với vận tốc 2 n vòng / phút thì cảm kháng của đoạn mạch AB là

• A\(\frac{R}{{\sqrt 3 }}\)
• BR\(\sqrt 3 \)        
• C\(\frac{{2R}}{{\sqrt 3 }}\)
• D2R\(\sqrt 3 \)

Đáp án: C

Lời giải cụ thể :

Đáp án C

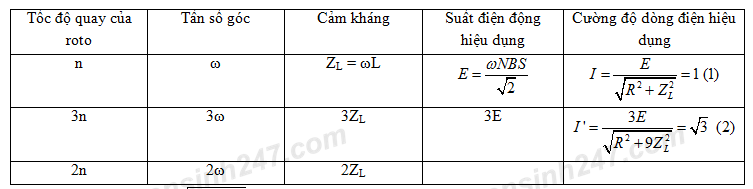
Từ (1) và (2) ta có: \(\frac{I}{{I’}} = \frac{{\sqrt {{R^2} + 9Z_L^2} }}{{3\sqrt {{R^2} + Z_L^2} }} = \frac{1}{{\sqrt 3 }}\,\, \Rightarrow {Z_L} = \frac{R}{{\sqrt 3 }}\)

=> Cảm kháng của đoạn mạch AB khi roto của máy quay đều với tốc độ 2n vòng/phút là: \(2{Z_L} = \frac{{2R}}{{\sqrt 3 }}\)

Đáp án – Lời giải Câu hỏi 35 :Nối hai cực của một máy phát điện xoay chiều một pha vào hai đầu đoạn mạch AB mắc tiếp nối đuôi nhau gồm tụ điện và điện trở thuần thì hiệu suất tiêu thụ của đoạn mạch là P1 và thông số hiệu suất của đoạn mạch là 0,6. Bỏ qua điện trở thuần của những cuộn dây của máy phát điện. Cho rôto của máy phát điện quay với vận tốc tăng gấp đôi thì hiệu suất tiêu thụ của đoạn mạch xê dịch bằng .

• A4,1 P1.   
• B1,9 P1.
• C7,7 P1. 
• D1,3 P1.

Đáp án: C

Lời giải cụ thể :

Đáp án C

Lúc đầu : \ ( \ cos { \ varphi _1 } = \ frac { R } { { \ sqrt { { R ^ 2 } + Z_C ^ 2 } } } = 0,6 = > { Z_C } = \ frac { 4 } { 3 } R \ ). Công suất tiêu thụ là \ ( { P_1 } = UI \ cos { \ varphi _1 } = \ frac { { { U ^ 2 } } } { R } { \ cos ^ 2 } { \ varphi _1 } \ )
Lúc sau vận tốc tăng 2 lần thì tần số là 2 f và U ’ = 2U
thì \ ( Z { ‘ _C } = \ frac { { { Z_C } } } { 2 } = \ frac { 4 } { 6 } R = > { \ cos ^ 2 } { \ varphi _2 } = \ frac { { { R ^ 2 } } } { { { R ^ 2 } + Z_C ^ 2 } } = \ frac { R } { { { R ^ 2 } + \ frac { { { 4 ^ 2 } } } { { { 6 ^ 2 } } } { R ^ 2 } } } = \ frac { 9 } { { 13 } } \ )
Công suất tiêu thụ của đoạn mạch là
\ ( \ begin { array } { l } { P_2 } = \ frac { { 4 { U ^ 2 } } } { R } { \ cos ^ 2 } { \ varphi _2 } \ \ \ frac { { { P_2 } } } { { { P_1 } } } = \ frac { { 4 { { \ cos } ^ 2 } { \ varphi _2 } } } { { { { \ cos } ^ 2 } { \ varphi _1 } } } = > { P_2 } = 4 { P_1 } \ frac { { { { \ cos } ^ 2 } { \ varphi _2 } } } { { { { \ cos } ^ 2 } { \ varphi _1 } } } = 4 { P_1 } \ frac { { \ frac { 9 } { { 13 } } } } { { 0,36 } } = 7,69 { P_1 } \ end { array } \ )Đáp án – Lời giải Câu hỏi 36 :Một máy phát điện xoay chiều với một khung dây có 1000 vòng, quay đều trong từ trường đều có B = 0,11 T, diện tích quy hoạnh mỗi vòng dây là 90 cm2, suất điện động cảm ứng trong khung có giá trị hiệu dụng là 220V. Chu kì của suất điện động là :

• A0,02s
• B0,028s
• C 0,014s
• D 0,01s

Đáp án: A

Phương pháp giải :

+ Vận dụng biểu thức tính biên độ suất điện động: \({E_0} = \omega NBS = \omega N{\Phi _0}\)

+ Vận dụng biêu thức tính chu kì : \ ( T = \ frac { { 2 \ pi } } { \ omega } \ )Lời giải cụ thể :

Đáp án A

Ta có :
+ Biên độ suất điện động :
\ ( { E_0 } = \ omega NBS \ to \ omega = \ frac { { { E_0 } } } { { NBS } } = \ frac { { E \ sqrt 2 } } { { NBS } } = \ frac { { 220 \ sqrt 2 } } { { 1000.0,11. ( { { 90.10 } ^ { – 4 } } ) } } = 314,27 ( ra { \ rm { d } } / s ) \ )
+ Chu kì : \ ( T = \ frac { { 2 \ pi } } { \ omega } = \ frac { { 2 \ pi } } { { 314,27 } } = 0,01999 \ approx 0,02 { \ rm { s } } \ )Đáp án – Lời giải Câu hỏi 37 :Hai máy phát điện xoay chiều một pha : máy thứ nhất có 2 cặp cực, rôto quay với vận tốc 1600 vòng / phút. Máy thứ hai có 4 cặp cực. Để tần số do hai máy phát ra như nhau thì rôto máy thứ hai quay với vận tốc là bao nhiêu ?

• A800 vòng/phút.  
• B400 vòng/phút.   
• C3200 vòng/phút.  
• D1600 vòng/phút

Đáp án: A

Phương pháp giải :Vận dụng biểu thức : \ ( f = \ frac { { Np } } { { 60 } } \ ) với N là số vòng / phút, p là số cặp cựcLời giải chi tiết cụ thể :

Đáp án A

ta có :
\ ( { f_1 } = \ frac { { { N_1 } { p_1 } } } { { 60 } } ; { f_2 } = \ frac { { { N_2 } { p_2 } } } { { 60 } } \ )
để \ ( { f_1 } = { f_2 } \ ) thì \ ( \ frac { { { N_1 } { p_1 } } } { { 60 } } = \ frac { { { N_2 } { p_2 } } } { { 60 } } \ to { N_2 } = \ frac { { { N_1 } { p_1 } } } { { { p_2 } } } = \ frac { { 1600.2 } } { 4 } = 800 \ ) ( vòng /Đáp án – Lời giải Câu hỏi 38 :Đặt một điện áp xoay chiều có trị hiệu dụng U = 100V vào hai đầu một động cơ điện xoay chiều thì hiệu suất cơ học của động cơ là 160W. Động cơ có điện trở thuần \ ( R = 4 \ Omega \ ) và thông số hiệu suất là 0,88. Biết hiệu suất của động cơ không nhỏ hơn 50 %. Cường độ dòng điện hiệu dụng qua động cơ là :

• A\(I{\rm{ }} = 2A\)   
• B\(I = 20A\)     
• C\(I = 2\sqrt 2 A\)   
• D\(I{\rm{ }} = 2A\)hoặc \(I = 20A\)

Đáp án: A

Lời giải cụ thể :

Đáp án A

Ta có :

\(\eqalign{
& {P_{tp}} = {\rm{ }}{P_{hp}} + {\rm{ }}{P_{co{\rm{ }}hoc}} \cr
& \to UIc{\rm{os}}\varphi {\rm{ = }}{{\rm{I}}^2}R + 160 \cr
& \leftrightarrow 100.0,88I = 4{I^2} + 160 \cr
& \to \left[ \matrix{
I = 2A \hfill \cr
I = 20A \hfill \cr} \right. \cr} \)

Vì hiệu suất của động cơ không nhỏ hơn 50 % nên => I = 2 AĐáp án – Lời giải Câu hỏi 39 :Một động cơ điện có ghi 220V-176 W, thông số hiệu suất bằng 0,8 được mắc vào mạch điện xoay chiều có điện áp hiệu dụng 380V. Để động cơ hoạt động giải trí thông thường, phải mắc động cơ tiếp nối đuôi nhau với một điện trở thuần có giá trị :

• A180W    
• B300W   
• C220W
• D 176W

Đáp án: A

Phương pháp giải :

+ Vận dụng biểu thức tính công suất: \(P = UIc{\rm{os}}\varphi \)

+ Vận dụng biểu thức : \ ( R = \ frac { { { U_R } } } { I } \ )Lời giải cụ thể :

Đáp án A

Ta có :
\ ( I = \ frac { { { P_ { dc } } } } { { { U_ { dc } } { \ rm { cos } } \ varphi } } = \ frac { { 176 } } { { 220.0,8 } } = 1 ( A ) \ )
\ ( \ begin { array } { l } U_ { mach } ^ 2 = U_ { dc } ^ 2 + U_R ^ 2 + 2 { U_ { dc } } { U_R } { \ rm { cos } } \ varphi \ \ \ leftrightarrow { \ rm { 38 } } { { \ rm { 0 } } ^ 2 } = { 220 ^ 2 } + U_R ^ 2 + 2.220. U_R ^ 2.0,8 \ \ \ to { U_R } = 180V \ end { array } \ )
vì dòng điện qua R cũng là dòng điện qua động cơ : \ ( \ to R = \ frac { { { U_R } } } { I } = \ frac { { 180 } } { 1 } = 180 \ Omega \ )Đáp án – Lời giải Câu hỏi 40 :Một máy phát điện xoay chiều một pha có ro to là một nam châm hút điện có một cặp cực, quay đều với vận tốc n ( vòng / phút ). Một đoạn mạch RLC tiếp nối đuôi nhau được mắc vào hai cực của máy. Khi roto quay với vận tốc n1 = 30 vòng / phút thì dung kháng của tụ điện bằng R ; khi roto quay với vận tốc n2 = 40 vòng / phút thì điện áp hiệu dụng ở hai đầu tụ điện đạt giá trị cực lớn. Bỏ qua điện trở thuần ở những cuộn dây phần ứng. Để cường độ dòng điện hiệu dụng qua mạch đạt giá trị cực lớn thì roto phải quay với vận tốc bằng

• A24 vòng/phút
• B34 vòng/phút
• C120 vòng/phút 
• D50 vòng/phút

Đáp án: C

Phương pháp giải :Suất điện động của nguồn điện : \ ( E = \ sqrt { 2 } \ omega N { { \ varphi } _ { 0 } } = \ sqrt { 2 }. 2 \ pi fN { { \ varphi } _ { 0 } } \ )
Với f = np, trong đó n là vận tốc quay của roto, p là số cặp cực từ .
Cảm kháng ZL = ωL
Dung kháng ZC = ( ωC ) – 1
Định luật Ôm cho đoạn mạch : I = U / ZLời giải cụ thể :Suất điện động của nguồn điện : \ ( E = \ sqrt { 2 } \ omega N { { \ varphi } _ { 0 } } = \ sqrt { 2 }. 2 \ pi fN { { \ varphi } _ { 0 } } \ )
Với f = np, trong đó n là vận tốc quay của roto, p là số cặp cực từ .
Do r = 0 nên điện áp hiệu dụng đặt vào hai đầu mạch U = E = kω
+ Khi n = n1 thì \ ( R = { { Z } _ { C1 } } = \ frac { 1 } { { { \ omega } _ { 1 } } C } \ ) ( 1 )
+ Khi n = n2
\ ( { { U } _ { C2 } } = I { { Z } _ { C2 } } = \ frac { k { { \ omega } _ { 2 } }. \ frac { 1 } { { { \ omega } _ { 2 } } C } } { \ sqrt { { { R } ^ { 2 } } + { { ( { { Z } _ { L } } – \ frac { 1 } { { { \ omega } _ { 2 } } C } ) } ^ { 2 } } } } \ )
=> UC2 = UC2 max khi ZL2 = ZC2 => \ ( \ omega _ { 2 } ^ { 2 } = \ frac { 1 } { LC } ( 2 ) \ )
+ Khi n = n3 thì \ ( I = \ frac { k { { \ omega } _ { 3 } } } { \ sqrt { { { R } ^ { 2 } } + { { ( { { Z } _ { L } } – { { Z } _ { C3 } } ) } ^ { 2 } } } } = \ frac { k { { \ omega } _ { 3 } } } { \ sqrt { { { R } ^ { 2 } } + { { ( { { \ omega } _ { 3 } } L – \ frac { 1 } { { { \ omega } _ { 3 } } C } ) } ^ { 2 } } } } = \ frac { k } { \ sqrt { Y } } \ )
Với \ ( Y = \ frac { { { R } ^ { 2 } } + \ omega _ { 3 } ^ { 2 } { { L } ^ { 2 } } – 2 \ frac { L } { C } + \ frac { 1 } { \ omega _ { 3 } ^ { 2 } { { C } ^ { 2 } } } } { \ omega _ { 3 } ^ { 2 } } = \ frac { 1 } { { { C } ^ { 2 } } }. \ frac { 1 } { \ omega _ { 3 } ^ { 4 } } + ( { { R } ^ { 2 } } – 2 \ frac { L } { C } ) \ frac { 1 } { \ omega _ { 3 } ^ { 2 } } + { { L } ^ { 2 } } \ )
Đặt X = 1 / ω32 => \ ( Y = \ frac { 1 } { { { C } ^ { 2 } } } { { X } ^ { 2 } } + ( { { R } ^ { 2 } } – \ frac { 2L } { C } ) X + { { L } ^ { 2 } } \ )
I ­ max khi Y min => Y ’ = 0
\ ( \ Rightarrow \ frac { 1 } { \ omega _ { 3 } ^ { 2 } } = \ frac { 1 } { \ omega _ { 2 } ^ { 2 } } – \ frac { 1 } { 2 \ omega _ { 1 } ^ { 2 } } \ Rightarrow \ frac { 1 } { n_ { 3 } ^ { 2 } } = \ frac { 1 } { n_ { 2 } ^ { 2 } } – \ frac { 1 } { 2 n_ { 1 } ^ { 2 } } \ Rightarrow { { n } _ { 3 } } = \ frac { \ sqrt { 2 } { { n } _ { 1 } } { { n } _ { 2 } } } { \ sqrt { 2 n_ { 1 } ^ { 2 } – n_ { 2 } ^ { 2 } } } = 120 \ ) vòng / phút

Chọn C

Đáp án – Lời giải Câu hỏi 41 :Nối hai đầu đoạn mạch chỉ có tụ điện vào hai cực của máy phát điện xoay chiều một pha. Điện trở của máy phát không đáng kể. Khi roto của máy quay với vận tốc n ( vòng / phút ) thì cường độ dòng điện hiệu dụng trong mạch là 0,5 A. Nếu roto của máy quay với vận tốc 2 n ( vòng / phút ) thì cường độ dòng điện hiệu dụng trong mạch là

• A2A
• B1A
• C0,5A
• D0,25A

Đáp án: A

Phương pháp giải :Liên hệ giữa tần số góc và tần số : ω = 2 πf
Suất điện động tự cảm có giá trị cực lớn : E ­ 0 = ωNBS
Máy phát điện một chiều có roton quay vận tốc n vòng / giây, có p cặp cực thì sinh ra dòng điện có tần số f = np
Dung kháng của tụ : ZC = ( ωC ) – 1
Biểu thức định luật Ôm cho toàn mạch có nguồn không có điện trở trong : I = E / ZLời giải cụ thể :Tần số dòng điện : \ ( \ omega = 2 \ pi f = \ frac { 2 \ pi np } { 60 } \ Rightarrow \ omega \ sim n \ )
Suất điện động hiệu dụng : \ ( E = \ frac { { { E } _ { 0 } } } { \ sqrt { 2 } } = \ frac { 2 \ pi npNBS } { 60 \ sqrt { 2 } } \ Rightarrow E \ sim n \ )
Khi roto quay n vòng / phút ta có : \ ( { { I } _ { 1 } } = \ frac { E } { { { Z } _ { C } } } = E \ omega C \ )
Khi roto quay 2 n vòng / phút ta có : \ ( { { I } _ { 2 } } = \ frac { 2E } { \ frac { { { Z } _ { C } } } { 2 } } = 4E \ omega C = 4 { { I } _ { 1 } } = 4.0,5 = 2A \ )

Chọn A

Đáp án – Lời giải Câu hỏi 42 :Nối hai cực của một máy phát điện xoay chiều một pha vào hai đầu của đoạn mạch chỉ chứa tụ điện C. Khi rôto quay đều với vận tốc n vòng / s thì cường độ dòng điện hiệu dụng qua tụ là \ ( 4I \ ). Để cường độ dòng điện hiệu dụng qua tụ là \ ( I \ ) thì vận tốc quay đều của roto là

• A\(0,25n\)
• B\(2n.\)
• C\(4n.\)
• D\(0,5n.\)

Đáp án: D

Phương pháp giải :+ Sử dụng biểu thức tính : \ ( U = \ omega NBS \ )
+ Sử dụng biểu thức tính dung kháng : \ ( { Z_C } = \ dfrac { 1 } { { \ omega C } } \ )
+ Sử dụng biểu thức tính cường độ dòng điện : \ ( I = \ dfrac { U } { { { Z_C } } } \ )Lời giải cụ thể :+ Khi roto quay với vận tốc \ ( n \ ) vòng / s thì :
\ ( U = 2 \ pi n. NBS \ )
\ ( { I_2 } = 4I = \ dfrac { U } { { { Z_C } } } = \ dfrac { { 2 \ pi n. NBS } } { { \ dfrac { 1 } { { 2 \ pi n. C } } } } = { \ left ( { 2 \ pi n } \ right ) ^ 2 } NBS \ )
+ Khi roto quay với vận tốc \ ( n ‘ \ ) vòng / s thì
\ ( { I_2 } = I = \ dfrac { U } { { { Z_C } ‘ } } = \ dfrac { { 2 \ pi n ‘. NBS } } { { \ dfrac { 1 } { { 2 \ pi n ‘. C } } } } = { \ left ( { 2 \ pi n ‘ } \ right ) ^ 2 } NBS \ )
\ ( \ dfrac { { { I_2 } } } { { { I_1 } } } = \ dfrac { I } { { 4I } } = { \ left ( { \ dfrac { { n ‘ } } { n } } \ right ) ^ 2 } \ Rightarrow n ‘ = \ dfrac { n } { 2 } \ )

Chọn D

Đáp án – Lời giải Câu hỏi 43 :Trong máy phát điện xoay chiều ba pha, mỗi pha có suất điện động cực lớn là \ ( { E_0 } \ ). Khi suất điện động tức thời ở cuộn 1 bị triệt tiêu thì giá trị suất điện động tức thời trong cuộn 2 và cuộn 3 tương ứng là \ ( { e_2 } \ ) và \ ( { e_3 } \ ) thỏa mãn nhu cầu hệ thức là

• A\({e_2}{e_3} =  – \dfrac{{E_0^2}}{4}.\)
• B\({e_2}{e_3} = \dfrac{{3E_0^2}}{4}.\)
• C\({e_2}{e_3} =  – \dfrac{{3E_0^2}}{4}.\)
• D\({e_2}{e_3} = \dfrac{{E_0^2}}{4}.\)

Đáp án: C

Phương pháp giải :Vận dụng biểu thức của suất điện động trong máy phát điện xoay chiều ba pha \ ( \ left \ { \ begin { array } { l } { e_1 } = { E_0 } cos \ left ( { \ omega t } \ right ) \ \ { e_2 } = { E_0 } cos \ left ( { \ omega t + \ dfrac { { 2 \ pi } } { 3 } } \ right ) \ \ { e_3 } = { E_0 } cos \ left ( { \ omega t – \ dfrac { { 2 \ pi } } { 3 } } \ right ) \ end { array } \ right. \ )Lời giải cụ thể :Ta có, biểu thức suất điện động của mỗi pha trong máy phát điện xoay chiều ba pha :
\ ( \ left \ { \ begin { array } { l } { e_1 } = { E_0 } cos \ left ( { \ omega t } \ right ) \ \ { e_2 } = { E_0 } cos \ left ( { \ omega t + \ dfrac { { 2 \ pi } } { 3 } } \ right ) \ \ { e_3 } = { E_0 } cos \ left ( { \ omega t – \ dfrac { { 2 \ pi } } { 3 } } \ right ) \ end { array } \ right. \ )
Khi suất điện động tức thời ở cuộn 1 bị triệt tiêu
\ ( { e_1 } = 0 \ Rightarrow cos \ omega t = 0 \ Rightarrow \ left | { \ sin \ omega t } \ right | = 1 \ )
\ ( { e_2 } = { E_0 } cos \ left ( { \ omega t + \ dfrac { { 2 \ pi } } { 3 } } \ right ) = { E_0 } \ left [ { cos \ left ( { \ omega t } \ right ) { \ rm { cos } } \ dfrac { { 2 \ pi } } { 3 } – \ sin \ omega t. \ sin \ dfrac { { 2 \ pi } } { 3 } } \ right ] = – { E_0 } sin \ left ( { \ omega t } \ right ) \ sin \ dfrac { { 2 \ pi } } { 3 } \ )
\ ( { e_3 } = { E_0 } cos \ left ( { \ omega t – \ dfrac { { 2 \ pi } } { 3 } } \ right ) = { E_0 } \ left [ { cos \ left ( { \ omega t } \ right ) { \ rm { cos } } \ dfrac { { 2 \ pi } } { 3 } + \ sin \ omega t. \ sin \ dfrac { { 2 \ pi } } { 3 } } \ right ] = { E_0 } sin \ left ( { \ omega t } \ right ) \ sin \ dfrac { { 2 \ pi } } { 3 } \ )
Do \ ( \ left | { \ sin \ omega t } \ right | = 1 \ ) \ ( \ Rightarrow { e_2 }. { e_3 } = \ dfrac { { – 3 } } { 4 } E_0 ^ 2 \ )

Chọn C

Đáp án – Lời giải Câu hỏi 44 :

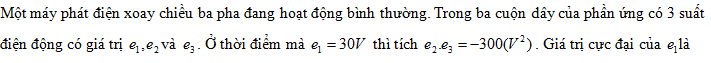
• A 50 V.         
• B40 V.
• C45 V.
• D35 V.

Đáp án: B

Lời giải cụ thể :

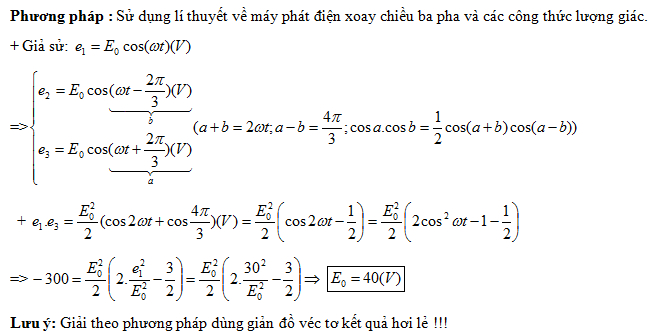
Đáp án – Lời giải Câu hỏi 45 :

Đặt điện áp xoay chiều u = U0cosωt (ω thay đổi được), vào hai đầu đoạn mạch R, C, L nối tiếp (cuộn dây thuần cảm). Khi ω = ω0 thì công suất tiêu thụ của mạch đạt cực đại, khi ω = ωL = 48π (rad/s) thì ULmax. Ngắt mạch ra khỏi điện áp xoay chiều nói trên rồi nối mạch vào hai cực của một máy phát điện xoay chiều một pha có điện trở trong không đáng kể, phần cảm là nam châm có 1 cặp cực. Khi tốc độ quay của rôto là n1 = 20 (vòng/s) hoặc n2 = 60 (vòng/s) thì điện áp hiệu dụng hai đầu cuộn cảm bằng nhau. Giá trị của ω0 gần nhất với giá trị nào sau đây?

• A161,52 rad/s. 
• B172,3 rad/s. 
• C156,1 rad/s. 
• D149,37 rad/s.

Đáp án: C

Lời giải cụ thể :Đáp án C
Ta có : \ ( \ omega _0 ^ 2 = { \ omega _L }. { \ omega _C } ; { \ omega _C } = \ sqrt { { 1 \ over { LC } } – { { { R ^ 2 } } \ over { 2 { L ^ 2 } } } } \ )
Ta có :

\(\left\{ \matrix{
{\omega _1} = 2\pi {f_1} = 2\pi {n_1}p = 40\pi (rad/s) \hfill \cr
{\omega _2} = 2\pi {f_2} = 2\pi {n_2}p = 120\pi (rad/s) \hfill \cr} \right.\)

Điện áp hiệu dụng hai đầu cuộn cảm : \ ( { U_L } = I. { Z_L } = { { E. { Z_L } } \ over { \ sqrt { { R ^ 2 } + { { \ left ( { { Z_L } – { Z_C } } \ right ) } ^ 2 } } } } = { { NBS { \ omega ^ 2 } L } \ over { \ sqrt 2 \ sqrt { { R ^ 2 } + { { \ left ( { { Z_L } – { Z_C } } \ right ) } ^ 2 } } } } \ )
Khi

\(\eqalign{
& {U_{{L_1}}} = {U_{{L_2}}} = > {{\omega _1^2} \over {\sqrt {{R^2} + {{\left( {{\omega _1}L – {1 \over {{\omega _1}C}}} \right)}^2}} }} = {{\omega _2^2} \over {\sqrt {{R^2} + {{\left( {{\omega _2}L – {1 \over {{\omega _2}C}}} \right)}^2}} }} \cr
& \Leftrightarrow {R^2} + {\left( {{\omega _2}L – {1 \over {{\omega _2}C}}} \right)^2} = 81{R^2} + 81{\left( {{\omega _1}L – {1 \over {{\omega _1}C}}} \right)^2} \cr
& \omega _2^2{L^2} – {{2L} \over C} + {1 \over {\omega _2^2{C^2}}} = 80{R^2} + 81\omega _1^2{L^2} – {{162L} \over C} + {{81} \over {\omega _1^2{C^2}}} \cr
& 160{L \over C} – 80{R^2} = \left( {81\omega _1^2 – \omega _2^2} \right){L^2} + {1 \over {{C^2}}}\left( {{{81} \over {\omega _1^2}} – {1 \over {\omega _2^2}}} \right) \cr
& 160{1 \over {LC}} – 80{{{R^2}} \over {{L^2}}} = \left( {81\omega _1^2 – \omega _2^2} \right) + {1 \over {{L^2}{C^2}}}\left( {{{81} \over {\omega _1^2}} – {1 \over {\omega _2^2}}} \right) \cr
& 160\left( {{1 \over {LC}} – {{{R^2}} \over {2{L^2}}}} \right) = \left( {81\omega _1^2 – \omega _2^2} \right) + {1 \over {{L^2}{C^2}}}\left( {{{81} \over {\omega _1^2}} – {1 \over {\omega _2^2}}} \right) \cr} \)

Lại có

\(\left\{ \matrix{
\omega _0^2 = {1 \over {LC}} \hfill \cr
\omega _C^2 = {1 \over {LC}} – {{{R^2}} \over {2{L^2}}} \hfill \cr} \right. = > 160\omega _C^2 = \left( {81\omega _1^2 – \omega _2^2} \right) + \omega _0^4\left( {{{81} \over {\omega _1^2}} – {1 \over {\omega _2^2}}} \right)\left( * \right)\)

Thay \ ( \ omega _0 ^ 2 = { \ omega _L }. { \ omega _C } \ ) vào ( * ) ta có : \ ( 160 { \ left ( { { { \ omega _0 ^ 2 } \ over { { \ omega _L } } } } \ right ) ^ 2 } = \ left ( { 81 \ omega _1 ^ 2 – \ omega _2 ^ 2 } \ right ) + \ omega _0 ^ 4 \ left ( { { { 81 } \ over { \ omega _1 ^ 2 } } – { 1 \ over { \ omega _2 ^ 2 } } } \ right ) \ )
Thay số ta có : \ ( 160 { \ left ( { { { \ omega _0 ^ 2 } \ over { 48 \ pi } } } \ right ) ^ 2 } = \ left ( { 81. { { \ left ( { 40 \ pi } \ right ) } ^ 2 } – { { \ left ( { 120 \ pi } \ right ) } ^ 2 } } \ right ) + \ omega _0 ^ 4 \ left ( { { { 81 } \ over { { { \ left ( { 40 \ pi } \ right ) } ^ 2 } } } – { 1 \ over { { { \ left ( { 120 \ pi } \ right ) } ^ 2 } } } } \ right ) = > { \ omega _0 } \ approx 156,12 rad / s \ )Đáp án – Lời giải Câu hỏi 46 :Nối hai cực của một máy phát điện xoay chiều một pha vào hai đầu đoạn mạch AB gồm điện trở thuần R mắc tiếp nối đuôi nhau với cuộn cảm thuần. Bỏ qua điện trở những cuộn dây của máy quay đều với vận tốc n vòng / phút thì cường độ dòng điện hiệu dụng trong đoạn mạch là 1 A. Khi ro to của máy quay đều với vận tốc 3 n vòng / phút thì cường độ dòng điện hiệu dụng trong đoạn mạch là \ ( \ sqrt 3 A \ ). Nếu rô to của máy quay đều với vận tốc 2 n / phút thì cường độ dòng điện hiệu dung trong mạch gần bằng

• A1,4 A
• B1,8 A
• C1,5 A
• D1,6 A

Đáp án: C

Phương pháp giải :Công thức tính suất điện động cực lớn : E0 = NBSω = NBS. 2 πf
Cường độ dòng điện : \ ( I = \ frac { E } { { \ sqrt { { R ^ 2 } + { { ( L2 \ pi f ) } ^ 2 } } } } \ )
Mà ta có f = p. n với n ( vòng / giây ) là vận tốc quay của rotoLời giải chi tiết cụ thể :Ta có : f = p. n
Suất điện động cực lớn : E0 = NBSω = NBS. 2 πf ;
Ta có :

\(\begin{array}{l}
\left\{ \begin{array}{l}
{I_1} = \frac{{NBS.2\pi .p.n}}{{\sqrt 2 \sqrt {{R^2} + {{(L2\pi p.n)}^2}} }} = 1\\
{I_2} = \frac{{NBS.2\pi .p.3n}}{{\sqrt 2 \sqrt {{R^2} + {{(L2\pi p.3n)}^2}} }} = \sqrt 3
\end{array} \right.\\
\Rightarrow \frac{{{I_2}}}{{{I_1}}} = \frac{3}{{\sqrt {{R^2} + {{(L2\pi p.3n)}^2}} }}.\sqrt {{R^2} + {{(L2\pi p.n)}^2}} = \sqrt 3 \\
\Rightarrow R = \sqrt 3 .(L2\pi p.n)\\
{I_3} = \frac{{NBS.2\pi .p.2n}}{{\sqrt 2 \sqrt {{R^2} + {{(L2\pi p.2n)}^2}} }}\\
\Rightarrow \frac{{{I_3}}}{{{I_1}}} = \frac{2}{{\sqrt 7 }}.\sqrt 4 = \frac{4}{{\sqrt 7 }} = 1,51A
\end{array}\)

Chọn C

Đáp án – Lời giải Câu hỏi 47 :

Một máy phát điện xoay chiều 3 pha đang hoạt động. Tại thời điểm t, điện áp tức thời ở cuộn thứ nhất gấp 2 lần điện áp tức thời ở cuộn thứ hai, còn điện áp tức thời ở cuộn thứ ba có độ lớn là 175 V.  Điện áp cực đại trên mỗi cuộn gần nhất với giá trị nào sau đây?

• A189 V.                       
• B181 V.        
• C186 V.   
• D178 V.

Đáp án: D

Phương pháp giải :

Phương pháp:

Biểu thức điện áp : \ ( \ left \ { \ begin { array } { l } { u_1 } = { U_0 } \ cos \ left ( { \ omega t + \ varphi } \ right ) \ \ { u_2 } = { U_0 } \ cos \ left ( { \ omega t + \ varphi + 120 } \ right ) \ \ { u_3 } = { U_0 } \ cos \ left ( { \ omega t + \ varphi – 120 } \ right ) \ end { array } \ right. \ )Lời giải cụ thể :

Cách giải:

Biểu thức điện áp : \ ( \ left \ { \ begin { array } { l } { u_1 } = { U_0 } \ cos \ left ( { \ omega t + \ varphi } \ right ) \ \ { u_2 } = { U_0 } \ cos \ left ( { \ omega t + \ varphi + 120 } \ right ) \ \ { u_3 } = { U_0 } \ cos \ left ( { \ omega t + \ varphi – 120 } \ right ) \ end { array } \ right. \ )
Đặt \ ( x = \ omega t + \ varphi \ Rightarrow \ left \ { \ begin { array } { l } { u_1 } = { U_0 } \ cos x \ \ { u_2 } = { U_0 } \ cos \ left ( { x + 120 } \ right ) \ \ { u_3 } = { U_0 } \ cos \ left ( { x – 120 } \ right ) \ end { array } \ right. \ )

Tại thời điểm t, điện áp tức thời ở cuộn thứ nhất gấp 2 lần điện áp tức thời ở cuộn thứ hai:

\(\begin{array}{l}{u_1} = 2{u_2} \Leftrightarrow \cos x = 2.\cos \left( {x + 120} \right)\\ \Leftrightarrow \cos x = 2.\left( {\cos x.\cos 120 – {\mathop{\rm s}\nolimits} {\rm{inx}}.\sin 120} \right)\\ \Leftrightarrow \cos x =  – \cos x + \sqrt 3 {\mathop{\rm s}\nolimits} {\rm{inx}}\\ \Rightarrow {\rm{tanx  =   – }}\frac{2}{{\sqrt 3 }} \Rightarrow x =  – 49,{1^0}\end{array}\)

Khi đó điện áp tức thời ở cuộn thứ ba có độ lớn là 175V. Ta có :

\(\begin{array}{l}\left| {{U_0}.\cos \left( {x – 120} \right)} \right| = 75 \Leftrightarrow \left| {{U_0}.\cos \left( { – 49,1 – 120} \right)} \right| = 75\\ \Rightarrow {U_0} = 178V\end{array}\)

Chọn D

Đáp án – Lời giải Câu hỏi 48 :Một máy phát điện xoay chiều một pha có điện trở trong không đáng kể. Nối hai cực của máy phát với một đoạn mạch gồm một điện trở mắc tiếp nối đuôi nhau với một cuộn cảm thuần. Khi rôto của máy phát quay đều với vận tốc góc là n vòng / s thì cường độ dòng điện hiệu dụng trong mạch là \ ( 2 \ sqrt 3 \ ) A và thông số hiệu suất của mạch bằng \ ( \ dfrac { { \ sqrt 3 } } { 2 }. \ ) Nếu rôto quay đều với vận tốc góc là 3 n vòng / s thì cường độ dòng điện hiệu dụng trong mạch là

• A\(4\sqrt 3 \) A.   
• B4 A.   
• C\(4\sqrt 2 \) A. 
• D6 A.

Đáp án: D

Phương pháp giải :Cảm kháng của cuộn dây : \ ( { Z_L } = \ omega L \ )
Hệ số hiệu suất của đoạn mạch xoay chiều : \ ( \ cos \ varphi = \ dfrac { R } { { \ sqrt { { R ^ 2 } + { Z_L } ^ 2 } } } \ )
Suất điện động hiệu dụng của máy phát điện : \ ( E = \ dfrac { { NBS \ omega } } { { \ sqrt 2 } } \ )
Cường độ dòng điện hiệu dụng : \ ( I = \ dfrac { E } { { \ sqrt { { R ^ 2 } + { Z_L } ^ 2 } } } \ )Lời giải chi tiết cụ thể :Khi rôto quay với vận tốc ꞷ = n vòng / s, thông số hiệu suất của mạch là :
\ ( \ begin { array } { l } \ cos \ varphi = \ dfrac { R } { { \ sqrt { { R ^ 2 } + { Z_L } ^ 2 } } } = \ dfrac { { \ sqrt 3 } } { 2 } \ Rightarrow 4 { R ^ 2 } = 3 { R ^ 2 } + 3 { Z_L } ^ 2 \ \ \ Rightarrow { R ^ 2 } = 3 { Z_L } ^ 2 \ Rightarrow { Z_L } = \ dfrac { R } { { \ sqrt 3 } } \ end { array } \ )
Cường độ dòng điện hiệu dụng trong mạch là :
\ ( I = \ dfrac { E } { { \ sqrt { { R ^ 2 } + { Z_L } ^ 2 } } } = 2 \ sqrt 3 \ Rightarrow \ dfrac { E } { { \ sqrt { { R ^ 2 } + \ dfrac { { { R ^ 2 } } } { 3 } } } } = 2 \ sqrt 3 \ Rightarrow E = 4R \ )
Khi quay với vận tốc ꞷ ’ = 3 n vòng / s, cảm kháng của cuộn dây và suất điện động hiệu dụng của máy phát là :
\ ( \ left \ { \ begin { array } { l } { Z_L } ‘ = 3 { Z_L } \ Rightarrow { Z_L } ‘ = R \ sqrt 3 \ \ E ‘ = 3E = 12R \ end { array } \ right. \ )
Cường độ dòng điện hiệu dụng trong mạch khi đó là :
\ ( I ‘ = \ dfrac { U } { { \ sqrt { { R ^ 2 } + { Z_L } { ‘ ^ 2 } } } } = \ dfrac { { 12R } } { { \ sqrt { { R ^ 2 } + { { \ left ( { \ sqrt 3 R } \ right ) } ^ 2 } } } } = 6 \, \, \ left ( A \ right ) \ )

Chọn D.

Đáp án – Lời giải Câu hỏi 49 :

Một máy phát điện xoay chiều ba pha đang hoạt động bình thường. Trong ba cuộn dây ở phần ứng có ba suất điện động có giá trị e1, e2 và e3. Ở thời điểm mà e1 = 35 V thì tích e2e3 = -1275 V2. Giá trị cực đại của e1 là

• A57,7 V                               
• B40V                                    
• C45V                                   
• D35V

Đáp án: A

Phương pháp giải :Suất điện động xoay chiều :

\(\left\{ \begin{array}{l}
{e_1} = {E_0}.\cos \left( {\omega t} \right)\\
{e_2} = {E_0}.\cos \left( {\omega t + \frac{{2\pi }}{3}} \right)\\
{e_3} = {E_0}.\cos \left( {\omega t – \frac{{2\pi }}{3}} \right)
\end{array} \right.\)

Lời giải cụ thể :Suất điện động xoay chiều :

\(\left\{ \begin{array}{l}
{e_1} = {E_0}.\cos \left( {\omega t} \right)\\
{e_2} = {E_0}.\cos \left( {\omega t + \frac{{2\pi }}{3}} \right)\\
{e_3} = {E_0}.\cos \left( {\omega t – \frac{{2\pi }}{3}} \right)
\end{array} \right.\)

Tích :

\(\begin{array}{l}
{e_2}.{e_3} = E_0^2.\frac{1}{2}.\left[ {\cos \left( {2\omega t} \right) + \cos \left( {\frac{{4\pi }}{3}} \right)} \right] = E_0^2.\frac{1}{2}.\left[ {2{{\cos }^2}\omega t – 1 – \frac{1}{2}} \right]\\
\Leftrightarrow {e_2}.{e_3} = E_0^2.{\cos ^2}\omega t – \frac{3}{4}E_0^2 = {\left( {{E_0}.\cos \omega t} \right)^2} – \frac{3}{4}E_0^2 = – 1275\\
\Leftrightarrow {\left( {35} \right)^2} – \frac{3}{4}E_0^2 = – 1275 \Rightarrow {E_0} = \frac{{100}}{{\sqrt 3 }}V \approx 57,{7_{}}V
\end{array}\)

Chọn A.

Đáp án – Lời giải Câu hỏi 50 :Nếu rôto quay tăng thêm 1 vòng / s thì tần số của dòng điện do máy phát tăng từ 60H z đến 70H z và suất điện động hiệu dụng do máy phát ra đổi khác 40V so với khởi đầu. Hỏi nếu liên tục tăng vận tốc của rôto thêm 1 vòng / s nữa thì suất điện động hiệu dụng do máy phát tạo ra là

• A320V.     
• B240V.            
• C400V.       
• D280V.     

Đáp án: A

Phương pháp giải :Suất điện động hiệu dụng của máy phát điện xoay chiều :
\ ( E = \ dfrac { { { E_0 } } } { { \ sqrt 2 } } = \ dfrac { { NBS \ omega } } { { \ sqrt 2 } } = \ dfrac { { NBS. 2 \ pi f } } { { \ sqrt 2 } } = \ dfrac { { NBS. 2 \ pi. np } } { { \ sqrt 2 } } \ Rightarrow E \ sim f \ sim n \ )Lời giải cụ thể :Suất điện động hiệu dụng của máy phát điện xoay chiều là :
\ ( E = \ dfrac { { { E_0 } } } { { \ sqrt 2 } } = \ dfrac { { NBS \ omega } } { { \ sqrt 2 } } = \ dfrac { { NBS. 2 \ pi f } } { { \ sqrt 2 } } = \ dfrac { { NBS. 2 \ pi. np } } { { \ sqrt 2 } } \ Rightarrow E \ sim f \ sim n \ )
Ta có : \ ( \ dfrac { { { n_1 } } } { { { n_1 } + 1 } } = \ dfrac { { 60 } } { { 70 } } \ Rightarrow { n_1 } = 6 \ )

\(\dfrac{{{n_1}}}{{{n_1} + 1}} = \dfrac{{{E_1}}}{{{E_1} + 40}} \Rightarrow {E_1} = 240\,\,\left( V \right)\)

Theo đề bài ta có :
\ ( \ dfrac { { { n_1 } } } { { { n_1 } + 2 } } = \ dfrac { { { E_1 } } } { { { E_3 } } } \ Rightarrow \ dfrac { 6 } { 8 } = \ dfrac { { 240 } } { { { E_3 } } } \ Rightarrow { E_3 } = 320 \, \, \ left ( V \ right ) \ )

Chọn A.

Đáp án – Lời giải

Source: https://vvc.vn
Category : Gia Dụng