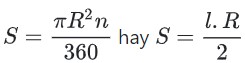I. Lý thuyết cần nắm về Diện tích hình tròn, hình quạt tròn
1. Diện tích hình tròn
Diện tích của một hình tròn với nửa đường kính R được tính theo công thức :
S = πR²
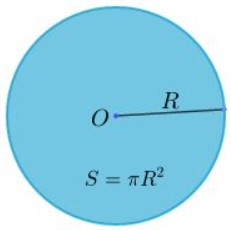
Trong đó :
- π là hằng số, π ≈ 3,14
- R là nửa đường kính của đường tròn .
Ví dụ: Tính diện tích hình tròn có đường kính là 13 cm.
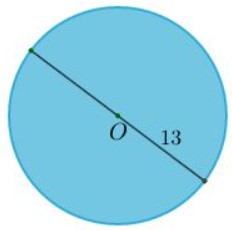
Ta có : R = 13 cm
=> Diện tích hình tròn là : S = πR² = π13² = 169 π ≈ 530,66 ( cm² )
2. Hình quạt tròn và Diện tích hình quạt tròn
a) Định nghĩa hình quạt nón
Hình quạt nón là một phần của hình tròn được số lượng giới hạn bởi một cung tròn và hai nửa đường kính đi qua hai mút của cung đó .
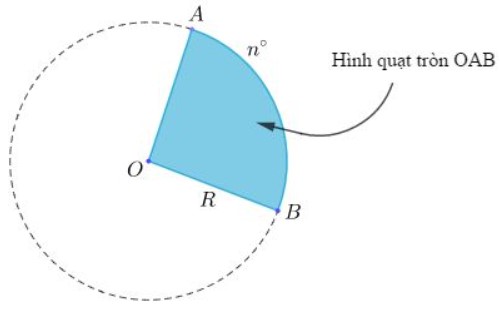
Ở hình trên, OAB là một hình quạt tròn có tâm O, nửa đường kính R và cung n ° .
b) Diện tích hình quạt tròn
Diện tích hình quạt tròn nửa đường kính E, cung n ° được tính theo công thức :
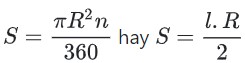
Trong đó :
- l là độ dài cung ;
- n ° là số đo của cung ;
- π là hằng số, π ≈ 3,14
- R là nửa đường kính của đường tròn .
Ví dụ: Tính diện tích của hình quạt tròn sau:
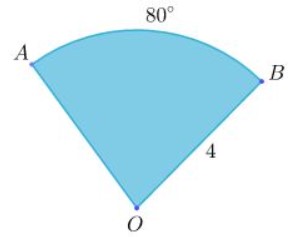
Cung tròn OAB với nửa đường kính R = 4, số đo cung n ° = 80 °
=> Diện tích là : S = ( π. R². n ° ) / 360 = ( π. 4 ². 80 ) / 360 = 32 π / 9 ≈ 12 .
II. Các dạng bài tập về Diện tích hình tròn, hình quạt tròn và cách giải giải chi tiết (Trắc nghiệm + Tự luận)
Chuyên đề Diện tích hình tròn, hình quạt tròn có 2 dạng bài tập chính là :
- Dạng 1 – Tính diện tích hình tròn, hình quạt tròn và các loại lương có liên quan
Để làm được dạng bài tập này, bạn cần vận dụng những công thức nêu ở phần I và những kiến thức và kỹ năng đã có .
- Dạng 2 – Một số bài toán tổng hợp
Đây là dạng có mức độ khó cao hơn dạng 1. Bạn cần sử dụng linh động những kỹ năng và kiến thức đã học để tìm được số đo góc ở tâm, độ dài nửa đường kính đường tròn. Từ hiệu quả đó, bạn sẽ tính được diện tích hình tròn và diện tích hình quạt tròn .
Sau đây là một số ít Bài tập trắc nghiệm + Bài tập tự luận về chuyên đề Diện tích hình tròn, hình quạt tròn có giải thuật cụ thể để những em học viên tìm hiểu thêm :
Bài tập trắc nghiệm
Câu 1: Một hình tròn có diện tích S= 225π (cm²). Bán kính của hình tròn đó là:
A. 15 (cm)
B. 16 (cm)
C. 12 (cm)
D. 14 (cm)
Lời giải:
Diện tích S = πR² = 225 π => R² = 225 = > R = 15 ( cm )
Vậy A là đáp án đúng
Câu 2: Diện tích hình tròn bán kính R = 10cm là:
A. 100π (cm²)
B. 10π (cm²)
C. 20π (cm²)
D. 100π² (cm²)
Lời giải:
Diện tích S = πR² = 10 ²π = 100 π ( cm² )
Vậy A là đáp án đúng
Câu 3: Cho đường tròn (O;10cm) với đường kính AB. Điểm M ∈ đường tròn (O) sao cho góc BAM = 45°. Tính diện tích hình quạt AOM.
A. 5π (cm²)
B. 25π (cm²)
C. 50π (cm²)
D. 25/2π (cm²)
Lời giải:
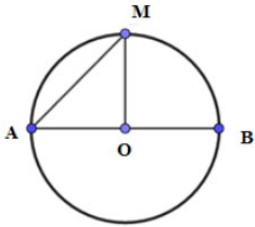
Xét đường tròn ( O ; 10 cm ) có :
=> ΔAMO là tam giác vuông cân => Góc MOA = 90 °
Vậy ta tính được diện tích hình quạt AOM là :
S = ( π. R². n ° ) / 360 = ( π. 10 ². 90 ) / 360 = 25 π ( cm² )
Vậy B là đáp án đúng
Câu 4: Cho đường tròn (O) với đường kính AB = 3√3. Điểm C ∈ O sao cho góc ABC = 60°. Tính diện tích của hình viên phân BC. (Phần hình tròn giới hạn bởi một cung tròn và dây căng cung ấy gọi là hình viên phân).
Lời giải:
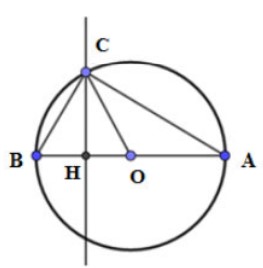
Xét đường tròn ( O ) có : Góc ACB = 90 ° ( Góc nội tiếp chắn nửa đường tròn )
=> Góc CAB = 90 ° – góc CBA = 60 ° ( Tam giác ABC vuông tại C )
Góc CAB và góc BOC là góc nội tiếp và góc ở tâm cùng chắn cung
=> Góc BOC = 2 lần Góc CAB = 2.30 ° = 60 °
=> Diện tích hình quạt AOC là : Sq = ( π. R². 60 ) / 360 = π. R² / 6
Xét tam giác AOC có :
- Góc BOC = 60 °
- OA = OC = R
=> Tam giác BOC đều có cạnh bằng R
Gọi đường cao của tam giác AOC là H, ta có :
CH = CO. Sin 60 ° = √ 3R / 2
=> Diện tích tam giác AOC là : S ΔaAOC = 50%. CH.OA = √ 3R ² / 4
Diện tích hình viên phân BC là : Diện tích hình quạt AOC – Diện tích tam giác BOC
⇔ π. R² / 6 – √ 3R ² / 4 = ( 18 π – 27 √ 3 ) / 16 ( cm² )
Bài tập tự luận
Bài 1: (77 / 98 / SGK TOÁN 9 T2)
Tính diện tích của hình tròn nội tiếp hình vuông vắn có độ dài cạnh là 4 cm .
Lời giải:
Khi giải bài này ta phải sử dụng công thức tính diện tích hình quạt tròn : S = πR²
Do hình vuông vắn có cạnh bằng 4 cm thì hình tròn nội tiếp hình vuông vắn này cũng có đường kính là 4 cm => R = d / 2 = 2 cm
=> Diện tích hình tròn là : S = πR² = π2² = 4 π ≈ 18,56 ( cm² )
Bài 2: (78 / 98 / SGK TOÁN 9 T2)
Chân của một đống cát đổ trên một nền phẳng nằm ngang có hình dạng là một hình tròn có chu vi 12 m. Hỏi chân đống cát đó chiếm diện tích bao nhiêu mét vuông ?
Lời giải:
Theo công thức tính diện tích hình tròn S = πR² thì muốn tính diện tích mà đống cát đã chiếm ta gọi R là nửa đường kính của đường tròn chân đống cát .
Ta có : 2 πR = 12 => R = 6 / π ( m )
Vậy diện tích đống cát đã chiếm sẽ là :
S = πR² = π. ( 6 / π ) ² ≈ 11,5 ( m² ) .
Bài 3: (80 / 98 / SGK TOÁN 9 T2)
Một vườn cỏ có hình dạng hình chữ nhật ABCD, cạnh AB = 40 m và AD = 30 m. Người ta muốn ở hai góc vườn A và B buộc hai con dê. Có hai cách buộc :
- Một dây thừng có độ dài 20 m
- Một dây thừng có độ dài 30 m và dây thừng kia có độ dài 10 m .
Hỏi cách buộc dây nào sẽ giúp diện tích cỏ mà cả hai con dê hoàn toàn có thể ăn được sẽ lớn hơn ?
Lời giải:
- Theo cách buộc thứ nhất :
Con dê hoàn toàn có thể di động trên diện tích bằng 1/4 hình tròn có nửa đường kính 20 m và tìm hoạt động giải trí của hai con dê chiếm diện tích bằng nhau .
Diện tích cỏ hai con dê ăn được : 20 ²π. 1/4. 2 = 200 π ( m² )
Diện tích cỏ con dê buộc ở vị trí A ăn được là : 1/4. π. 30 ² = 225 π ( m² )
Diện tích cỏ con dê buộc ở vị trí B ăn được là : 1/4. π. 10 ² = 25 π ( m² )
Diện tích cỏ cả hai con dê ăn được : 225 π + 25 π = 250 π ( m² )
Do đó buộc theo cách thứ hai thì diện tích cỏ mà hai con dê ăn được sẽ lớn hơn cách buộc thứ nhất
Bài 4: (83 / 99 / SGK TOÁN 9 T2)
a) Vẽ hình dưới đây (tạo bởi các cung tròn) với HI = 10cm; HO = BI = 2cm. Nêu cách vẽ ?
b) Tính diện tích hình HOABINH màu đậm
c) Chứng minh hình tròn đường với kính NA có diện tích bằng diện tích của hình HOABINH đó.
Lời giải:
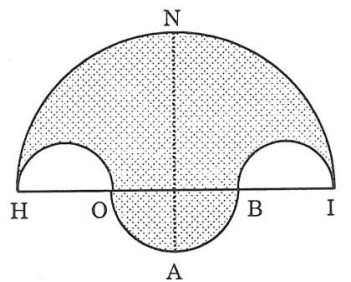
a) Cách vẽ hình HOABINH
– Vẽ một nửa đường tròn với đường kính HI = 10 cm .
– Vẽ cùng một phía so với IH hai nửa đường tròn đường kính HO = IB = 2 cm .
– Vẽ nửa đường tròn đường kính HB = 6 cm nằm ở phía dưới so với nửa đường tròn đường kính HI .
b) Tính diện tích hình HOABINH
Diện tích hình HOABINH gồm diện tích nửa hình tròn đường kính HI = 10 cm và diện tích nửa hình tròn đường kính OB = 6 cm. Trừ đi diện tích hai nửa hình tròn đường kính HO và đường kính BI. Do đó ta có :
1/2.π.5² + 1/2.π.3² + 1/2.π.1².2 = 16π (cm²)
c) Tính diện tích hình tròn với đường kính NA:
S = π. 4 ² = 16 π ( cm² )