Con lắc lò xo là triết lý quan trọng trong chương trình Vật Lý lớp 12. Trong bài này, Luật Minh Khuê sẽ giúp những bạn mạng lưới hệ thống lại bài học kinh nghiệm con lắc lò xo .
Con lắc lò xo là một hệ gồm một vật nặng kích cỡ nhỏ có khối lượng m gắn vào một đầu của lò xo, có độ cứng k, đầu còn lại của lò xo được gắn hoặc treo vào một điểm cố định và thắt chặt. Có thể sắp xếp cho con lắc lò xo xê dịch theo phương ngang, theo phương thẳng đứng hoặc theo phương của một dốc nghiêng .
Dựa theo định nghĩa trên ta có 3 loại con lắc lò xo :
2. Cấu tạo của con lắc lò xo
Con lắc lò xo gồm một vật nhỏ có khối lượng m gắn vào đầu của một lò xo có độ cứng k, có khối lượng không đáng kể. Đầu kia của lò xo được giữ cố định và thắt chặt. Vật m hoàn toàn có thể trượt trên một mặt phẳng nằm ngang không có ma sát .
Vị trí cân đối của vật là vị trí khi lò xo không biến dạng. Vật sẽ đứng yên mãi ở vị trí này nếu lúc đầu nó đứng yên .
Kéo vật ra khỏi vị trí cân đối cho lò xo dãn ra một đoạn nhỏ rồi buông tay, ta thấy vật giao động trên một đoạn thẳng quanh vị trí cân đối .
3. Khảo sát dao động của con lắc lò xo về mặt động lực học
Chọn trục tọa độ x song song với trục của lò xo, chiều dương là chiều tăng độ dài l của lò xo. Chọn gốc tọa độ O tại vị trí cân đối. Giả sử vật có li độ x .
Vì trọng lực phản lực của mặt phẳng tác dụng vào vật cân bằng nhau, nên hợp lực tác dụng vào vật chỉ là lực đàn hồi của lò xo. Hơn nữa, ở vị trí vật có li độ x thì độ biến dạng của lò xo cũng bằng x(delta l = x). Do đó lực đàn hồi của lò xo Fđh = k.Δl có thể viết dưới dạng đại số như sau:
F = ma = – kx hay a = ( k / m ). x
Trong đó :
- F: là lực tác dụng lên m (N)
- x: là li độ của vật (m)
- k: độ cứng của lò xo (N/m)
Dấu ( – ) trong công thức bộc lộ rằng lực F luôn hướng về vị trí cân đối .
Ta có : w2 = k / m => a + w2. x = 0
Dao động của con lắc lò xo là giao động điều hòa theo phương trình. Tần số góc và chu kì của con lắc lò xo lần lượt là :
Lực luôn hướng về vị trí cân đối gọi là lực kéo về. Lực kéo về có độ lớn tỉ lệ với li độ và là lực gây ra tần suất cho vật xê dịch điều hòa .
Ngoài ra những bạn hoàn toàn có thể tìm hiểu thêm bảng công thức về con lắc lò xo dưới đây và áo dụng để giải những bài tập :
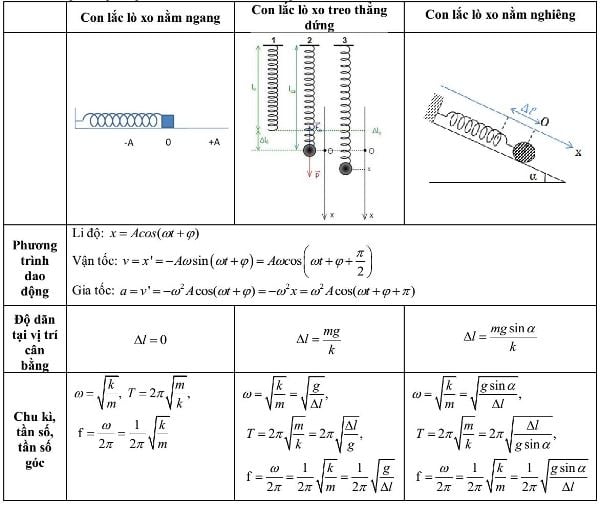
Bảng tổng hợp những công thức về những dạng con lắc lò xo
4. Khảo sát dao động của con lắc lò xo về mặt năng lượng
4.1 Động năng của con lắc lò xo
Động năng của con lắc lò xo là động năng của vật m :
wđ = 1/2. mv2
4.2 Thế năng của con lắc lò xo
Ở lớp 10 ta đã biết, khi lò xo bị biến dạng thì hệ gồm lò xo và vật nhỏ, tức là con lắc lò xo, có thế năng đàn hồi Wt = 1/2.k (Δl^2) .
Thay Δl = x vào ta có công thức tính thế năng của con lắc lò xo như sau:
Wt = 1/2.k.x2
4.3 Cơ năng của con lắc lò xo. Sự bảo toàn cơ năng
– Cơ năng của con lắc lò xo là tổng động năng và thế năng của con lắc .
W = 1/2. m. v2 + 50%. k. x2
– Ta hoàn toàn có thể chứng tỏ rằng khi không có ma sát thì cơ năng của con lắc được bảo toàn. Nó chỉ đổi khác từ dạng thế năng sang động năng và ngược lại .
W = 1/2. k. A2 = 1/2. m. w2. A2 = const
Cơ năng của con lắc lò xo luôn được bảo toàn và tỉ lệ với bình phương biên độ xê dịch .
- Nếu tại t1 ta có x1, v1 và tại t2 ta có x2, v2. Ta có thể tính được : tần số góc
- Nếu cho k, m và W, ta có thể tính được:
Lưu ý :
– Một vật giao động điều hòa với tần số góc, chu kỳ luân hồi T và tần số f thì động năng và thế năng biến thiên tuần hoàn với tần số góc w ‘, tần số f ‘ và chu kỳ luân hồi T ‘, mối liên hệ như sau :
w ‘ = 2 w, T ‘ = T / 2, f ‘ = 2 f .
- Khoảng thời gian ngắn nhất giữa hai lần liên tiếp động năng bằng thế năng là T/4y
- Khoảng thời gian 2 lần liên tiếp động năng bằng thế năng bằng không là T/2
– Khi con lắc lò xo giao động mà chiều dài của lò xo đổi khác từ chiều dài cực tiểu lmin đến chiều dài cực lớn lmax thì :
- Biên độ: A = (lmax – lmin)/2
- Chiều dài lúc cân bằng: lcb = lo + delta l = (lmax + lmin)/2
5. Một số bài tập liên quan
5.1. Dạng 1: Tính chu kỳ, tần số của Con lắc lò xo
Ví dụ 1: Một lò xo có độ cứng là K. Khi gắn vật m1 vào lò xo và cho dao động thì chu kỳ dao động là 0,3s. Khi gắn vật có khối lượng m2 vào lò xo trên và kích thích cho dao động thì nó dao động với chu kỳ là 0,4s. Hỏi nếu khi gắn vật có khối lượng m = 2m1 + 3m2 thì nó dao động với chu kỳ là bao nhiêu?
A. 0,25 s
B. 0,4 s
C. 0,812 s
D. 0,3 s
Hướng dẫn giải:
Xác định chu kỳ luân hồi xê dịch của vật khi gắn vật có khối lượng m = a. m1 + b. m2 :
=> T2 = a. T12 + b. T22 ⇔ T = căn. ( 2. T12 + 3. T22 ) = 0,812 s .
Ví dụ 2: Một con lắc lò xo nằm ngang có độ cứng K = 100 N/m được gắn vào vật nặng có khối lượng m = 0,1kg. Kích thích cho vật dao động điều hòa, xác định chu kỳ của con lắc lò xo? Lấy pi bình phương = 10.
A. 0,1 s
B. 5 s
C. 2 s
D. 0,3 s
Hướng dẫn giải:
Ta có :
T = 2 pi. căn ( m / k ) với m = 100 g = 0,1 kg ; k = 100. N / m
=> T = 2 pi. căn ( 0,1 / 100 ) = 2 s
5.2. Dạng 2: Tính chiều dài con lắc lò xo, lực đàn hồi, lực phục hồi
Ví dụ 1: Một con lắc lò xo có chiều dài tự nhiên là lo = 30 cm, độ cứng của lò xo và k = 10 N/m. Treo vật nặng có khối lượng m = 0,1 kg vào lò xo và kích thích cho lò xo dao động điều hòa theo phương thẳng đứng với biên độ A = 5 cm. xác định chiều dài cực đại, cực tiểu của lò xo trong quá trình dao động của vật.
A. 40 cm ; 30 cm
B. 45 cm ; 25 cm
C. 35 cm ; 55 cm
D. 45 cm ; 35 cm
Hướng dẫn giải:
Ta có : lo = 30 cm và delta lo = mg / k = 0,1 m = 10 cm
lmax = lo + delta lo + A = 30 + 10 + 5 = 45 cm
lmin = lo + delta lo – A = 30 + 10 – 5 = 35 cm
Ví dụ 2: Một con lắc lò xo có chiều dài tự nhiên là lo = 30 cm, độ cứng của lò xo là k = 10 N/m. Treo vật nặng có khối lượng m = 0,1 kg vào lò xo và kích thích cho lò xo dao động điều hòa theo phương thẳng đứng với biên độ A = 5 cm. Xác định lực đàn hồi cực đại, cực tiểu của lò xo trong quá trình dao động của vật.
A. 1,5 N ; 0,5 N
B. 2N ; 1,5 N
C. 2,5 N ; 0,5 N
D. Khác
Hướng dẫn giải:
Ta có : delta lo = 0,1 m > A
Áp dụng Fdhmax = K. ( A + delta lo ) = 10. ( 0,1 + 0,05 ) = 1,5 N
Fdhmin = k. ( A – delta lo ) = 10. ( 0,1 – 0,05 ) = 0,5 N
5.3. Dạng 3: Tính năng lượng của Con lắc lò xo
Ví dụ 1: Một con lắc lò xo đặt nằm ngang gồm vật m và lò xo có độ cứng k = 100N/m. Kích thích để vật dao động điều hòa với động năng cực đại 0,5J. Biên độ dao động của vật là
A. 50 cm
B. 1 cm
C. 10 cm
D. 5 cm
Hướng dẫn giải:
Ta có : E = Etmax = 1/2. k. A2 => A = căn. ( 2E / k ) = 0,1 m = 10 cm
Ví dụ 2: Khoảng thời gian ngắn nhất giữa hai lần Ed = Et khi một vật dao động điều hòa là 0,05s. Tần số dao động của vật là
A. 2,5 Hz
B. 3,75 Hz
C. 5H z
D. 5,5 Hz
Hướng dẫn giải:
Ta có : Khoảng thời hạn hai lần liên tục để động năng bằng thế năng là t = T / 4 = 0,05 s
=> T = 0,2 s => f = 1 / T = 5 Hz







