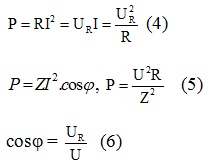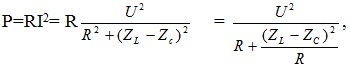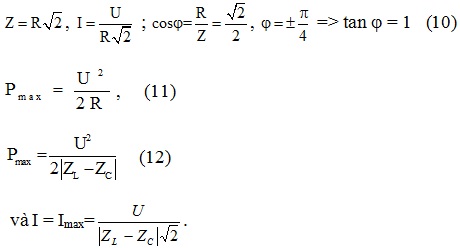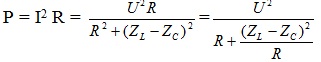I.Công suất tiêu thụ trong mạch RLC không phân nhánh:
+ Công suất tức thời : P = UIcosφ + UIcos ( 2 ωt + φ ) ( 1 )+ Công suất trung bình : P = UIcosφ = RI2 .+ Công suất tiêu thụ của mạch điện xoay chiều : P = UIcosφ ( 2 )+ Hệ số công suất : Cos φ = \ ( \ frac { R } { Z } \ ) ( Cos φ có giá trị từ 0 đến 1 ) ( 3 )+ Biến đổi ở những dạng khác :
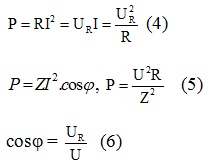
II. Ý nghĩa của hệ số công suất cosφ
+ Trường hợp cosφ = 1 -> φ = 0 : mạch chỉ có R, hoặc mạch RLC có cộng hưởng điện( ZL = ZC ) thì : P = Pmax = UI = \ ( \ frac { U ^ { 2 } } { R } \ ). ( 7 )+ Trường hợp cosφ = 0 tức là φ = ± \ ( \ frac { \ pi } { 2 } \ ) : Mạch chỉ có L, hoặc C, hoặc có cả L và C mà không có Rthì : P = Pmin = 0 .+ Công suất hao phí trên đường dây tải là : Php = rI2 = \ ( \ frac { rP ^ { 2 } } { U ^ { 2 } cos ^ { 2 } \ varphi } \ ) ( 8 )Với r ( Ω ) điện trở của đường dây tải điện .+ Từ ( 8 ) => Nếu cosj nhỏ thì Php lớn, do đó người ta phải tìm cách nâng cao cosφ. Quy định cosφ ≥ 0,85 .+ Với cùng một điện áp U và dụng cụ dùng điện tiêu thụ một công suất P, tăng cosφ để giảm cường độ hiệu dụng I từ đó giảm được hao phí vì tỏa nhiệt trên dây .+ Để nâng cao thông số công suất cosj của mạch bằng cách thường mắc thêm tụ điện thích hợp vào mạch điện sao cho cảm kháng và dung kháng của mạch xê dịch bằng nhau để cosφ ≈ 1 .
III.Các dạng bài tập:
1.Bài tập cơ bản:
Câu 1: Cho hiệu điện thê hai đầu đoạn mạch là :\(U_{AB}=10\sqrt{2}cos(100\pi t-\frac{\pi }{4})(V)\) và cường độ dòng điện qua mạch :\(i=3\sqrt{2}cos(100\pi t+\frac{\pi }{12})(A)\). Tính công suất tiêu thụ của đoạn mạch?
A. P = 180 ( W ) B. P = 120 ( W ) C. P = 100 ( W ) D. P = 50 ( W )
Bài giải : Ta có : \ ( I = \ frac { I_ { 0 } } { \ sqrt { 2 } } = \ frac { 3 \ sqrt { 2 } } { \ sqrt { 2 } } = 3 ( A ) \ ). \ ( U = \ frac { U_ { 0 } } { \ sqrt { 2 } } = \ frac { 120 \ sqrt { 2 } } { \ sqrt { 2 } } = 120 ( V ) \ ) Mặt khác : \ ( \ varphi _ { u } – \ varphi _ { i } = \ varphi \ rightarrow \ varphi = 100 \ pi t – \ frac { \ pi } { 4 } – ( 100 \ pi t + \ frac { \ pi } { 12 } ) = – \ frac { \ pi } { 3 } \ ) Vậy \ ( cos \ varphi = cos ( – \ frac { \ pi } { 3 } ) = \ frac { 1 } { 2 } \ )Suy ra công suất tiêu thụ của đoạn mạch là : \ ( P = UIcos \ varphi = 120.3. \ frac { 1 } { 2 } = 180 ( W ) \ )
Chọn A
2.R thay đổi để P =Pmax

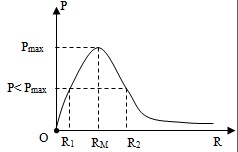
Khi L,C, ω không đổi thì mối liên hệ giữa ZL và ZC không thay đổi nên sự thay đổi của R không gây ra hiện tượng cộng hưởng
+ Tìm công suất tiêu thụ cực đại của đọan mạch:
Ta có
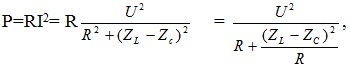
Do U = Const nên để P = Pmax thì ( \ ( R + \ frac { ( Z_ { L } – Z_ { C } ) ^ { 2 } } { R } \ ) ) đạt giá trị minÁp dụng bất dẳng thức Cosi cho 2 số dương R và ( ZL-ZC ) 2 ta được :
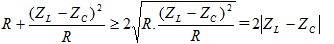
Vậy ( \ ( R + \ frac { ( Z_ { L } – Z_ { C } ) ^ { 2 } } { R } \ ) ) min là \ ( 2 \ left | Z_ { L } – Z_ { C } \ right | \ ) lúc đó dấu “ = ” của bất đẳng thức xảy ra nên ta có \ ( R = \ left | Z_ { L } – Z_ { C } \ right | \ )
Khi đó:
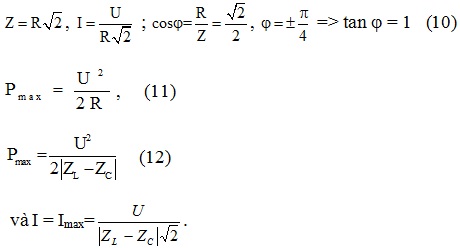
a. Các Ví dụ :
Ví dụ 1 : Cho mạch điện như hình vẽ:

\ ( L = \ frac { 1 } { \ pi } H, C = \ frac { 2.10 ^ { – 4 } } { \ pi } F \ ), uAB = 200 cos100πt ( V ) .
R phải có giá trị bằng bao nhiêu để công suất toả nhiệt trên R là lớn nhất ? Tính công suất đó.
A. 50 Ω ; 200W B. 100 Ω ; 200W C. 50 Ω ; 100W D. 100 Ω ; 100W
Giải: Ta có :ZL = ωL = 100 Ω; ZC = \(\frac{1}{\omega C}\)= 50 Ω; U = 100\(\sqrt{2}\)V
Công suất nhiệt trên R :
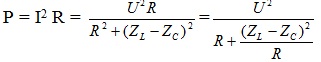
Theo bất đẳng thức Cosi : Pmax khi R = \ ( \ frac { ( Z_ { L } – Z_ { C } ) ^ { 2 } } { R } \ ) hay \ ( R = \ left | Z_ { L } – Z_ { C } \ right | = 50 \ Omega \ Rightarrow P_ { max } = \ frac { U ^ { 2 } } { 2R } = 200W \ )
Chọn A.
2. R thay đổi để có công suất P (P Có hai giá trị R1, R2 đều cho công suất P < Pmax
2.1. Tìm R để mạch có công suất P :
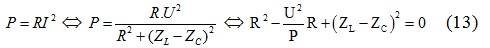
Vậy R là nghiệm của phương trình bậc hai, thuận tiện giải phương trình để được tác dụng có 2 nghiệm : R1 và R2
–Theo Định lý Viet ta có: R1 + R2 = \(\frac{U^{2}}{P}\) (14)
và R1.R2 = (ZL – ZC)2 (15)
a.Các Ví dụ :
+Ví dụ 3: Cho doạn mạch RLC mắc nối tiếp: cuộn dây thuần cảm kháng có độ tự cảm L= \(\frac{1}{\pi }H\), tụ điện có điện dung C= \(\frac{10^{-4}}{2\pi }\)F, R là một điện trở thuần thay đổi được. Đặt một hiệu điện thế xoay chiều ổn định ở hai đầu đoạn mạch AB có biểu thức: uAB=200cos100πt (V). Xác định R để mạch tiêu thụ công suất 80W.
A. 50Ω, 200Ω. B. 100Ω, 400Ω. C. 50Ω, 200Ω. D. 50Ω, 200Ω.
HD: Tính ZL= 100Ω, ZC= 200Ω, theo (13):\(R^{2}-\frac{U^{2}}{P}R+(Z_{L}-Z_{C})^{2}=0\) => R=50Ω và R=200Ω.
Chọn C.
2.2. Biết hai giá trị của điện trở là R1 và R2 mạch có cùng công suất P, tìm công suất P.

Ví dụ 9. Đặt vào hai đầu một điện trở thuần một hiệu điện thế xoay chiều có giá trị cực đại U0 công suất tiêu thụ trên R là P. Khi đặt vào hai đầu điện trở đó một hiệu điện thế không đổi có giá trị U0 thì công suất tiêu thụ trên R là
A. P B. 2P C.\(\sqrt{2}\)P D. 4P
Giải: Khi đặt hiệu điện thế xoay chiều thì P = I2R = \(\frac{U^{2}}{R}=\frac{{U_{0}}^{2}}{2R}\) (1)
Khi đặt hiệu điện thế không đổi thì P ’ = I2R = \ ( \ frac { { U_ { 0 } } ^ { 2 } } { R } \ ) ( 2 )
Suy ra: \(\frac{P’}{P}=2\) => P’ = 2P.
Chọn B
3. Công suất tiêu thụ cực đại khi mạch RLC có cộng hưởng.
Nếu giữ không đổi điện áp hiệu dụng U giữa hai đầu đoạn mạch và thay đổi tần số góc ω (hoặc thay đổi f, L, C) sao cho \(\omega L=\frac{1}{\omega C}\) (hay ZL=ZC) thì có hiện tượng cộng hưởng điện.

Điều kiện xảy ra hiện tượng kỳ lạ cộng hưởng trong mạch RLC nối tiếp :\ ( Z_ { L } = Z_ { C } ; \ omega L = \ frac { 1 } { \ omega C } ; \ omega = \ frac { 1 } { \ sqrt { LC } } \ ) ( 18 )
Lúc mạch có cộng hưởng thì:
Tổng trở : Z = Zmin = R ; UR = URmax = U ( 19 )Cường độ dòng điện : \ ( I = I_ { max } = \ frac { U } { R } \ ) ( 20 )Công suất của mạch khi có cộng hưởng đạt giá trị cực lớn :\ ( U = U_ { max } = \ frac { U ^ { 2 } } { R } \ ) ( 21 )Mạch có cộng hưởng thì điện áp cùng pha với cường độ dòng điện, nghĩa là :φ = 0 ; φu = φi ; cosφ = 1 ( 22 )Điện áp giữa hai điểm M, B chứa L và C đạt cực tiểuULCmin = 0. ( 23 )
Lưu ý: L và C mắc liên tiếp nhau
Tất cả nội dung bài viết. Các em hãy xem thêm và tải file chi tiết dưới đây: