Cách bấm máy tính để giải bài toán số phức nhanh chóng, chính xác – https://vvc.vn

ĐỪNG BỎ LỠ 1 số mẫu Sạc dự phòng có tiện ích sạc nhanh đang được giảm giá tại TGDĐ:

Kỳ thi THPT Quốc gia đang đến gần, dù bạn có chọn khối thi nào thì toán học cũng là môn thi chính. Trong đó, số phức lại là một chương vô cùng quan trọng. Vậy bạn đã biết cách bấm máy tính cầm tay để giải bài toán số phức nhanh chóng, chính xác? Cùng tham khảo bài viết dưới đây nhé!

1. Số phức là gì?

Bạn đang đọc: Cách bấm máy tính để giải bài toán số phức nhanh chóng, chính xác – https://vvc.vn

– Khái niệm số phức

Số phức (z) (tiếng Anh: Complex number) là số được viết dưới dạng z = a + bi, trong đó a, b là các số thực, i là đơn vị ảo và được quy ước i2 = -1 hay √i = -1

Ví dụ : 2 + 5 i -> phần thực : 2, phần ảo : 5

Số phức

– Một số khái niệm quan trọng trong trường số phức:

+ Dạng đại số của số phức: Mỗi số phức z đều được biểu diễn duy nhất dưới dạng: z = a + bi; trong đó a, b là các số thực.

+ Mặt phẳng phức: Đây là mặt phẳng tọa độ (Oxy) trong đó Ox (trục hoành) là trục thực, Oy là trục ảo.

+ Số thực và số thuần ảo: Z là số thuần ảo khi a = 0, z = bi. Ngược lại, z là số thực khi b = 0; z = a.

+ Số phức liên hợp: Số phức liên hợp sẽ có dạng như hình dưới đây.

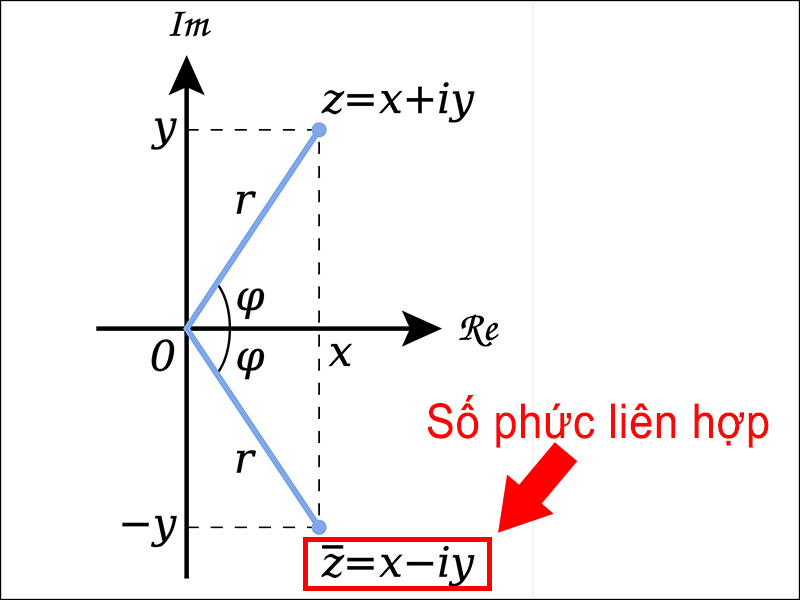
Số phức phối hợp
Lưu ý : Số phức phối hợp còn được viết tắt dưới dạng z * .

+ Module (Môđun) và Argument

– Căn bậc hai của z x z * được gọi là Môđun của z, ký hiệu là | z | .

– Argumen của số phức z, ký hiệu là arg(z) được thể hiện dưới hình dưới đây: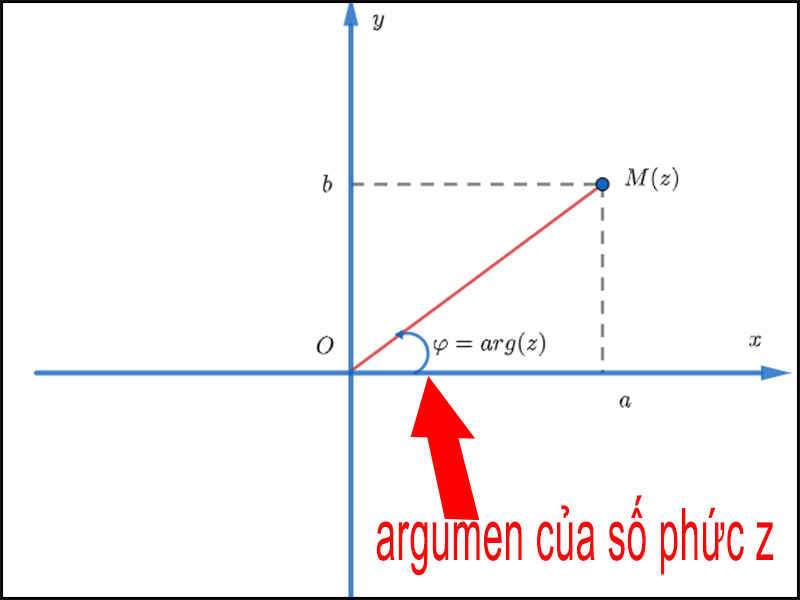

Khái niệm argumen của số phức z

2. Cách bấm máy tính số phức

Để tính số phức trên máy tính cầm tay, bạn cần thiết lập môi trường tính toán số phức bằng cách bấm phím MODE + 2. Khi đó, ở góc bên trên màn hình máy tính có chữ CMPLX có nghĩa môi trường số phức đã được thiết lập và bạn có thể thực hiện bấm máy như một phép tính bình thường.

Cách bấm máy tính số phức
SĂN NGAY MÃ GIẢM SỐC TGDĐ TẠI ĐÂY ! !

3. Cách giải bài toán số phức trên máy tính cầm tay

Các cách bấm phím với số phức:

Tính năng	Cách bấm
Phần ảo ( i )	Bấm phím ENG
Lấy Mođun số phức ( | z | )	Bấm Shift + hyp
Số phức phối hợp ( z )	Bấm Shift + 2 + 2
Argument	Bấm Shift + 2 + 1
Lấy phần thực của số phức	Bấm Shift + 2 + 3
Lấy phần ảo của số phức	Bấm Shift + 2 + 4
Đổi sang dạng lượng giác	Bấm Shift + mũi tên dưới + 1
Đổi sang dạng số	Bấm Shift + mũi tên dưới + 2

Một số bài toán ví dụ:

– Phương trình bậc nhất

Xem thêm: Quy định về kiểm định máy móc thiết bị

Để tính phương trình bậc nhất của số phức z, ta rút z ra sau đó bạn triển khai nhập phương trình máy để triển khai phép tính .

Ví dụ minh họa: Tìm số phức z thỏa mãn: z(2-i) = 5(3-2i).

Lời giải :

Bước 1: Ta biến đổi phương trình về dạng z = 5(3-2i) / (2-i)

Bước 2: Ta bấm Mode 2 để chuyển máy tính về môi trường số phức và nhập phương trình trên vào máy. Bấm dấu = để ra kết quả.

Phương trình bậc nhất của số phức z
Vậy z = 8 – i

– Phương trình bậc 2

Cách tính phương trình bậc 2 với thông số phức cũng được giải tựa như như phương trình bậc 2 với hệ số thực .

Ví dụ minh họa: Tính nghiệm của phương trình bậc hai Z2 + 2Z + 2=0

Lời giải :

Bước 1: Ta bấm MODE + 5 và bấm 3 để nhập phương trình bậc 2: ax2 + bx + c=0

Bấm phương trình bậc 2 trên máy tính cầm tay

Bước 2: Nhập a = 1; b = 2; c = 2 và bấm 2 lần dấu = để ra nghiệm x1 và x2.

Phương trình bậc 2 của số phức z
Vậy phương trình có 2 nghiệm là Z1 = – 1 + i và Z2 = – 1 – i

– Phương trình bậc 4

Vì máy tính chỉ tính được phương trình bậc 2 và 3 nên để tính được phương trình bậc 4 bạn cần chuyển phương trình về phương trình trùng phương .

Ví dụ minh họa: Tính nghiệm của phương trình Z4 – Z2 – 12=0

Lời giải :

Bước 1: Ta đặt Z2 = t > Phương trình (t) có dạng: t2 – t – 12 = 0

Bước 2: Bấm MODE + 5 và bấm 3 để nhập phương trình bậc 2: ax2 + bx + c = 0

Bấm phương trình bậc 2

Bước 3: Nhập a = 1; b = -1; c = -12 và bấm dấu =. Ta thu được 2 nghiệm của phương trình: t = 4 và t = -3 hay Z2 = 4 và Z2 = -3.

Hai nghiệm của phương trình t
+ Với Z2 = 4 => Z = ± 2
+ Với Z2 = – 3 => Z2 = 3 i2 ( vì i2 = – 1 ) => Z = ± √ ( 3 ) i

– Số phức liên hợp

Để tính số phức liên hợp z ta tính như phương trình bậc nhất của số phức z bằng cách rút z và bấm Shift + 2 + 2 để chuyển về dạng số phức liên hợp (z*).

Ví dụ minh họa: Tìm z* biết z = (3i – 2)/(i+1)

Lời giải :

Cách tính: Ta bấm Shift + 2 + 2 > Bấm trực tiếp phương trình vào trong máy tính > Bấm dấu = để ra kết quả.

Xem thêm: Tiêu chuẩn Việt Nam TCVN 5639:1991 Nguyên tắc cơ bản nghiệm thu thiết bị đã lắp đặt xong

Bấm phương trình số phức phối hợp

Bài viết trên đây đã hướng dẫn bạn cách bấm máy tính để giải bài toán số phức nhanh gọn, đúng chuẩn. Chúc các bạn triển khai thành công xuất sắc ! Cảm ơn và hẹn gặp lại các bạn ở những bài viết sau !

Source: https://vvc.vn
Category : Thiết Bị